题目内容
【题目】如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=![]() ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.

【答案】DE+BF=EF,见解析
【解析】
试题分析:通过延长CF,将DE和BF放在一起,便于寻找等量关系,通过两次三角形全等证明,得出结论.
猜想:DE+BF=EF.证明:延长CF,作∠4=∠1,如图:
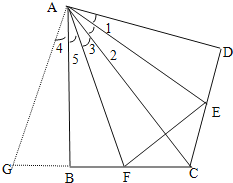
∵将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=∠DAB,
∴∠1+∠2=∠3+∠5,∠2+∠3=∠1+∠5,
∵∠4=∠1,
∴∠2+∠3=∠4+∠5,
∴∠GAF=∠FAE,
在△AGB和△AED中,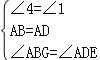 ,
,
∴△AGB≌△AED(ASA),
∴AG=AE,BG=DE,
在△AGF和△AEF中,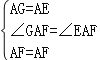 ,
,
∴△AGF≌△AEF(SAS),
∴GF=EF,
∴DE+BF=EF.
证毕.

练习册系列答案
相关题目