题目内容
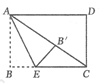
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠,点
折叠,点![]() 落点为
落点为![]() ,当
,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________;在折叠过程中,
的长为__________;在折叠过程中,![]() 的最小值为__________.
的最小值为__________.
【答案】![]() 或3 1
或3 1
【解析】
(1)先根据直角三角形的定义分两种情况:![]() 和
和![]() ,再根据折叠的性质、矩形的判定与性质分别得出点
,再根据折叠的性质、矩形的判定与性质分别得出点![]() 的位置,然后分别根据折叠的性质、勾股定理、矩形的性质求解即可得BE的长;
的位置,然后分别根据折叠的性质、勾股定理、矩形的性质求解即可得BE的长;
(2)利用折叠的性质、三角形的三边关系定理即可得.
(1)由直角三角形的定义,分以下两种情况:
①当![]() 时,
时,![]() 为直角三角形
为直角三角形
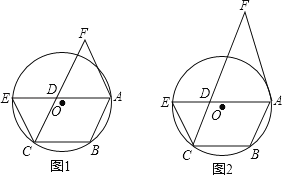
如图1,连接AC
![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,![]()
![]() ,
,![]()
由折叠的性质可知,![]()
![]()
![]() 点
点![]() 共线,即
共线,即![]() 沿AE折叠时,点B的对应点
沿AE折叠时,点B的对应点![]() 落在对角线AC上
落在对角线AC上
![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]() ,即
,即![]()

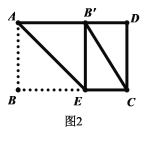
②当![]() 时,
时,![]() 为直角三角形
为直角三角形
![]()
![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,![]()
![]() ,
,![]()
由折叠的性质可知,![]()
![]() 四边形
四边形![]() 和四边形
和四边形![]() 均为矩形
均为矩形
![]() ,
,![]()
![]()
![]() 点
点![]() 共线,即
共线,即![]() 沿AE折叠时,点B的对应点
沿AE折叠时,点B的对应点![]() 落在边AD上
落在边AD上
则![]()
综上,BE的长为![]() 或3
或3
故答案为:![]() 或3;
或3;
(2)由折叠和矩形的性质得:![]() ,
,![]()
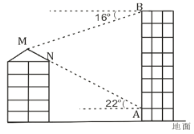
如图3-1,在折叠过程中,当点![]() 不落在边AD上时,点
不落在边AD上时,点![]() 总能构成一个三角形,即
总能构成一个三角形,即![]()
由三角形的三边关系定理得:![]()
如图3-2,在折叠过程中,当点![]() 恰好落在边AD上时,点
恰好落在边AD上时,点![]() 共线
共线
此时,![]()
综上,![]() 的取值范围为
的取值范围为![]()
则![]() 的最小值为1
的最小值为1
故答案为:1.


练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目