题目内容
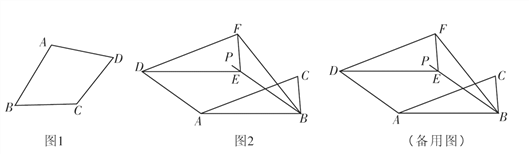
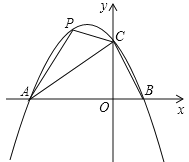
【题目】如图1,已知点A,B,C是⊙O上的三点,以AB,BC为邻边作ABCD,延长AD,交⊙O于点E,过点A作CE的平行线,交CD的延长线于F.
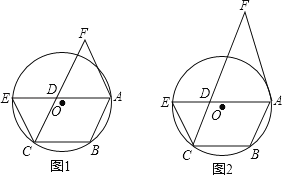
(1)求证:FD=FA;
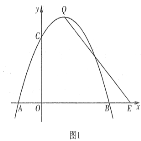
(2)如图2,连接AC,若∠F=40°,且AF恰好是⊙O的切线,求∠CAB的度数.
【答案】(1)见解析;(2)∠CAB=30°.
【解析】
(1)连接CA,如图1,先证明∠1=∠2得到弧CE=弧AB,则弧EB=弧AC,所以∠BAE=∠E,然后证明∠3=∠4得到FA=FD;
(2)连接OA、OC,如图2,利用三角形内角和计算出∠FAD=∠FDA=70°,再根据平行线的性质得到∠E=∠FAD=70°,∠BAD=∠FDA=70°,接着根据圆周角定理得到∠AOC=2∠E=140°,利用等腰三角形的性质得到∠OAC=20°,然后利用切线的性质得到∠OAF=90°,于是计算∠BAF-∠OAF-∠OAC即可.
(1)证明:连接CA,如图1,
∵四边形ABCD为平行四边形,
∴AE//BC,AB//CF,
∴∠1=∠2,
∴弧CE=弧AB,
∴弧CE+弧BC=弧AB+弧BC,即弧EB=弧AC,
∴∠BAE=∠E,
∵AB//CF,
∴∠4=∠BAE,
∵AF//CE,
∴∠E=∠3,
∴∠3=∠4,
∴FA=FD;
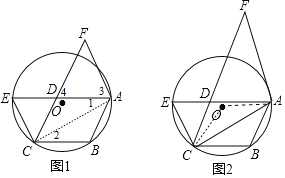
(2)解:连接OA、OC,如图2,
∵∠F=40°,
∴∠FAD=∠FDA=70°,
∴∠E=∠FAD=70°,∠BAD=∠FDA=70°,
∵∠AOC=2∠E=140°,∠BAF=∠FAD+∠BAD =140°,
而OC=OA,
∴∠OAC=![]() (180°﹣140°)=20°,
(180°﹣140°)=20°,
∵AF为切线,
∴OA⊥AF,
∴∠OAF=90°,
∴∠CAB=∠BAF﹣∠OAF﹣∠OAC=140°﹣90°﹣20°=30°.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案【题目】南宁海吉星水果批发市场李大姐家的水果店销售三华李,根据前段时间的销售经验,每天的售价![]() (元/箱)与销售量
(元/箱)与销售量![]() (箱)有如表关系,且已知
(箱)有如表关系,且已知 ![]() 与 x 之间的函数关系是一次函数.
与 x 之间的函数关系是一次函数.
每箱售价x(元) | 68 | 67 | 66 | 65 | … | 40 |
每天销量y(箱) | 40 | 45 | 50 | 55 | … | 180 |
(1)求y 与x的函数解析式;
(2)三华李的进价是 40 元/箱,如果设每天获得的盈利为 ![]() 元,要使该店每天获得最大盈利,则每箱售价多少元?
元,要使该店每天获得最大盈利,则每箱售价多少元?
(3)4 月份(按 30 天算)连续阴雨,销售量减少.该店决定采取降价销售,故在(2)的条件下销售了 18 天之后,三华李开始降价,售价比之前下降了![]() ,同时三华李的进价降为 29 元/箱,销售量也因此比原来每天获得最大盈利时上涨了
,同时三华李的进价降为 29 元/箱,销售量也因此比原来每天获得最大盈利时上涨了![]() ,降价销售了 12 天的三华李销售总盈利比降价销售前的销售总盈利少 5670 元,求
,降价销售了 12 天的三华李销售总盈利比降价销售前的销售总盈利少 5670 元,求![]() 的值.
的值.