Question

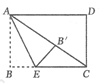
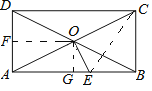
【题目】如图，已知矩形ABCD的对角线AC、BD相交于点O，过O点作OE⊥AC，交AB于E，若BC=4，△AOE的面积是5，则下列说法错误的是（ ）

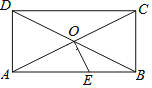
A.AE=5B.∠BOE=∠BCEC.CE⊥OBD.sin∠BOE=0.6

Answer 1

【答案】C

【解析】

过点O作OF⊥AD于F，作OG⊥AB于G，构建矩形AGOF，求出OG的长，利用三角形的面积公式可求得AE的长，进而可判断选项A；通过证明E、B、C、O四点共圆，进而可判断选项B；由E、B、C、O四点共圆，根据垂径定理可知，要想OB⊥CE，通过判断弦长BE和OE的大小即可，进而可判断选项C；利用同角的三角函数计算，进而可判断选项D．

A、过O作OF⊥AD于F，作OG⊥AB于G，

∵四边形ABCD是矩形，

∴AC＝BD，OA＝AC，OD＝BD，

∴OA＝OD，

∴AF＝FD＝AD＝BC＝2，

∵∠AGO＝∠BAD＝∠AFO＝90°，

∴四边形AGOF是矩形，

∴OG＝AF＝2，

∵S△AEO＝AEOG＝5，

∴AE＝5，

所以此选项的说法正确；

B、连接CE，∵OE⊥AC，

∴∠EOC＝90°

∵∠ABC＝90°，

∴∠ABC+∠EOC＝180°，

∴E、B、C、O四点共圆，

∴∠BCE＝∠BOE，

所以此选项的说法正确；

C、在Rt△BEC中，由勾股定理得：BE＝，

∴AB＝3+5＝8，

∴AC＝，

∴AO＝AC＝，

∴EO＝，

∴OE≠BE，

∵E、B、C、O四点共圆，

∵∠EOC＝90°，

∴EC是直径，

∴EC与OB不垂直；

此选项的说法不正确；

D、sin∠BOE＝sin∠BCE＝，

所以此选项的说法正确，

因为本题选择说法错误的，

故选C．