题目内容
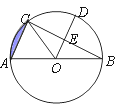
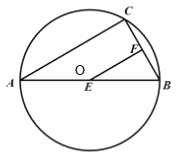
【题目】如图，AB是⊙O的直径，弦BC=4cm，点F是弦BC的中点，∠ABC=60°，若动点E以2cm/s的速度在线段AB上由A向B运动，连接EF，设运动时间为t(s)，当△BEF是直角三角形时，t的值等于______.
【答案】2s或
s．
【解析】
求出∠C=90°，求出AB，分为两种情况：画出图形，根据图形求出移动的距离即可．
∵动点E以2cm/s的速度从A点出发沿着A→B的方向运动．
∵AB是⊙O直径，∴∠C=90°．
∵F为BC中点，BC=4cm，∴BF=CF=2cm．
∵∠C=90°，∠B=60°，∴∠A=30°，∴AB=2BC=8cm．
分为两种情况：
①当∠EFB=90°时．
∵∠C=90°，∴∠EFB=∠C，∴AC∥EF．
∵FC=BF，∴AE=BE，即E和O重合，AE=4，t=4÷2=2（s）；
②当∠FEB=90°时．
∵∠ABC=60°，∴∠BFE=30°，∴BE=
BF=1，AE=8﹣1=7，t=7÷2=（s）．
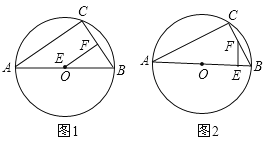
故答案为：2s或s．
练习册系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
