题目内容
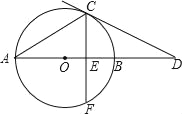
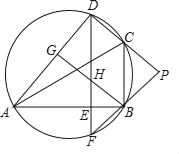
【题目】如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AB=![]() DH,∠COD=23°,求∠P的度数.
DH,∠COD=23°,求∠P的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)97°
【解析】
(1)根据邻补角定义和圆内接四边形对角互补、等边对等角即可证出结论.
(2)根据等边对等角得:∠PCB=∠PBC,由圆内接四边形的性质得:∠BAD+∠BCD=180°,从而得:∠BFD=∠PCB=∠PBC,根据平行线的判定得:BC∥DF,可得∠ABC=90°,AC是⊙O的直径,从而得:∠ADC=∠AGB=90°,根据同位角相等可得结论;
(3)先证明四边形BCDH是平行四边形,得BC=DH,根据特殊的三角函数值得:∠ACB=60°,最后由PC=PB,得出∠P=180°﹣2×(![]() )°=97°.
)°=97°.
(1)证明:如图1,
∵PC=PB,
∴∠PCB=∠PBC,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB;
(2)证明:由(1)得∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∵∠ABC=90°,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(3)解:由(1)得:BC∥DF,BG∥CD,
∴四边形BCDH是平行四边形,
∴BC=DH,
在Rt△ABC中,
∵AB=![]() DH,
DH,
∴tan∠ACB=![]() =
=![]() ,
,
∴∠ACB=60°,
连接OD,
∵∠COD=23°,OD=OC,
∴∠OCD=![]() (180°﹣23°)=(
(180°﹣23°)=(![]() )°,
)°,
∴∠PCB=180°﹣∠ACB﹣∠OCD=(![]() )°,
)°,
∵PC=PB,
∴∠P=180°﹣2×(![]() )°=97°.
)°=97°.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案【题目】某个体小服装店主准备在夏季来临前,购进甲、乙两种T恤.两种T恤的相关信息如表:
品牌 | 甲 | 乙 |
进价(元/件) | 45 | 80 |
售价(元/件) | 75 | 120 |
根据上述信息,该店决定用不少于6198元,但不超过6296元的资金购进这两种T恤共100件请解答下列问题:
(1)该店有哪几种进货方案?
(2)该店按哪种方案进货所获利润最大,最大利润是多少?