题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() ,得到
,得到![]() .
.
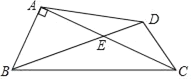
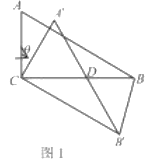
(1)如图1,当![]() 时,设
时,设![]() 与
与![]() 相交于点
相交于点![]() ,求证
,求证![]() 是等边三角形;
是等边三角形;
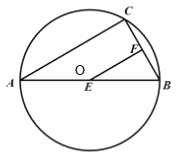
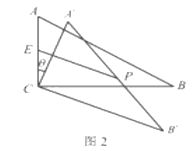
(2)如图2,设![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,
,![]() ,连接
,连接![]() .在旋转过程中,线段
.在旋转过程中,线段![]() 的长度是否存在最大值?如果存在,请求出这个最大值并说明此时旋转角
的长度是否存在最大值?如果存在,请求出这个最大值并说明此时旋转角![]() 的度数,如果不存在,请说明理由.
的度数,如果不存在,请说明理由.
【答案】(1)见详解;(2)线段EP的长度存在最大值,最大值EP=![]() ,θ=120°
,θ=120°
【解析】
(1)首先利用平行线的性质和旋转不变性可证得∠BCB=∠CBA=∠CBA=30°,据此可求得∠ACD、∠ADC,至此即可证明结论;
(2)连接CP,根据旋转的性质可得∠A=∠A=90°-30°=60°,AC=AC,根据题意可得
CP=![]() ,CE=
,CE=![]()
![]() ,至此在△ECP中,根据三角形的三边关系进行求解即可
,至此在△ECP中,根据三角形的三边关系进行求解即可
解:(1)证明:根据旋转的性质可得∠CBA=∠CBA=30°
∵AB//CB
∴∠BCB=∠CBA=30°,
∴∠ACB=90°,∠CAB=60°,
∵∠ACD+∠BCB=90°
∴∠ACB=60°
∴△ACD是等边三角形;
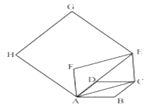
(2)存在.理由如下:
如解图1,连接CP,根据旋转的性质可得
∠A=∠A=90°-30°=60°, AC=AC
∵∠A=60°,AB中点为P,AC=![]() , AC=AC,
, AC=AC,
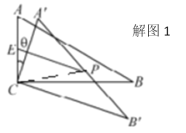
∴CP=![]() AB=
AB=![]() ·2
·2![]() =
=![]()
∴在△ECP中,EP<EC+CP=![]()
![]() +
+![]() =
=![]()
即EP<![]()
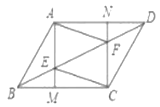
∴当E、F、C共线时,如解图2, PE最长
∴∠ACA=180°-∠PCA=180°-60°=120°
∴EP最长为![]() ,旋转角θ为120°.
,旋转角θ为120°.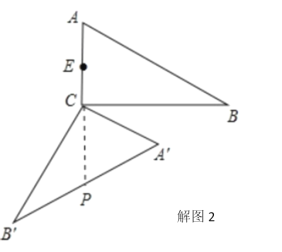

练习册系列答案
相关题目