题目内容
【题目】顺次连接四边形各边中点所得的四边形叫中点四边形.回答下列问题:
(1)只要原四边形的两条对角线______,就能使中点四边形是菱形;
(2)只要原四边形的两条对角线______,就能使中点四边形是矩形;
(3)请你设计一个中点四边形为正方形,但原四边形又不是正方形的四边形,把它画出来.
【答案】(1)相等;(2)垂直;(3)见解析
【解析】
(1)根据菱形的判定定理即可得到结论;
(2)根据矩形的判定定理即可得到结论;
(3)根据三角形的中位线平行于第三边并等于第三边的一半,先判断出AC=BD,又正方形的四个角都是直角,可以得到正方形的邻边互相垂直,然后证出AC与BD垂直,即可得到四边形ABCD满足的条件.
解:(1)顺次连接对角线相等的四边形的四边中点得到的是菱形;
(2)顺次连接对角线垂直的四边形的四边中点得到的是矩形;
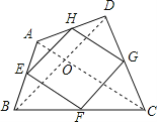
(3)如图,已知点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,AC=BD且AC⊥BD,
则四边形EFGH为正方形,
∵E、F分别是四边形ABCD的边AB、BC的中点,
∴EF∥AC,EF=![]() AC,
AC,
同理,EH∥BD,EH=![]() BD,GF=
BD,GF=![]() BD,GH=
BD,GH=![]() AC,
AC,
∵AC=BD,
∴EF=EH=GH=GF,
∴平行四边形ABCD是菱形.
∵AC⊥BD,
∴EF⊥EH,
∴四边形EFGH是正方形,
故顺次连接对角线相等且垂直的四边形的四边中点得到的四边形是正方形,
故答案为:相等,垂直.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案【题目】小冬与小夏是某中学篮球队的队员,在最近五场球赛中的得分如下表所示:
第一场 | 第二场 | 第三场 | 第四场 | 第五场 | |
小冬 |
|
|
|
|
|
小夏 |
|
|
|
|
|
(1)根据上表所给的数据,填写下表:
平均数 | 中位数 | 众数 | 方差 | |
小冬 |
|
|
| |
小夏 |
|
|
|
(2)根据以上信息,若教练选择小冬参加下一场比赛,教练的理由是什么?
(3)若小冬的下一场球赛得分是![]() 分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(
分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(![]() )
)