题目内容
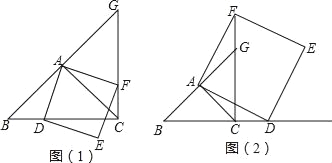
【题目】如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点.已知∠AEG=∠AGE,∠DCG=∠DGC.

(1) 求证:AB∥CD
(2) 若∠AGE+∠AHF=180°,且∠BFC-30°=2∠C,求∠B的度数
【答案】(1)见解析;(2)50°
【解析】
(1)根据对顶角相等,结合已知条件得出内错角相等,即可得两直线平行;
(2)根据对顶角相等,结合已知条件得出同旁内角互补,则可证出BF∥EC,根据平行线性质得出∠BFC与∠C的关系,结合已知条件求出∠BFC的度数,由两直线平行,同旁内角互补求∠B的度数.
解:(1)∵∠AEG=∠AGE,∠DCG=∠DGC,∠AGE=∠DGC,
∴∠AEG=∠DCG,
∴AB∥CD;
(2)∵∠AGE+∠AHF=180°,∠AGE=∠DGC,
∴∠CGD+∠AHF=180°,
∴BF∥EC;
∴∠BFC+∠C=180°,
∵∠BFC-30°=2∠C,
∴∠BFC=130°,
∵AB∥CD,
∴∠BFC+∠B=180°,
∴∠B=50°.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
【题目】如图所示的是用棋子摆成的“![]() ”字形图案.
”字形图案.

(1)填写下表:
图案序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子的个数 | 5 | 8 | … |
(2)第![]() 个“
个“![]() ”字形图案中棋子的个数为______.(用含
”字形图案中棋子的个数为______.(用含![]() 的代数式表示)
的代数式表示)
(3)第20个“![]() ”字形图案共有棋子多少个?
”字形图案共有棋子多少个?
(4)计算前20个“![]() ”字形图案中棋子的总个数为______
”字形图案中棋子的总个数为______