题目内容
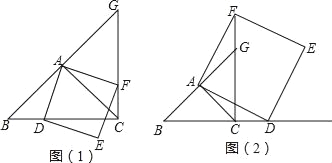
【题目】 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.
(1)求证:四边形ADCE是平行四边形;
(2)在△ABC中,若AC=BC,则四边形ADCE是 ;(只写结论,不需证明)
(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.

【答案】(1)证明见解析;(2)矩形;(3)证明见解析.
【解析】
(1)证明是平行四边形的方法有很多,此题用一组对边平行且相等较为简单,在平行四边形的基础上只需一个角是直角即可.
(2)根据矩形的判定解答即可.
(3)根据正方形的判定解答即可.
证明:(1)∵四边形BCED是平行四边形,
∴BD∥CE,BD=CE;
∵D是AB的中点,
∴AD=BD,
∴AD=CE;
又∵BD∥CE,
∴四边形ADCE是平行四边形.
(2)在△ABC中,若AC=BC,则四边形ADCE是矩形,
故答案为:矩形;
(3)∵AC⊥BC,
∴∠ACB=90°;
∵在Rt△ABC中,D是AB的中点,
∴CD=AD=![]() AB;
AB;
∵在△ABC中,AC=BC,D是AB的中点,
∴CD⊥AB,
∴∠ADC=90°;
∴平行四边形ADCE是正方形.

练习册系列答案
相关题目
【题目】如图所示的是用棋子摆成的“![]() ”字形图案.
”字形图案.

(1)填写下表:
图案序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子的个数 | 5 | 8 | … |
(2)第![]() 个“
个“![]() ”字形图案中棋子的个数为______.(用含
”字形图案中棋子的个数为______.(用含![]() 的代数式表示)
的代数式表示)
(3)第20个“![]() ”字形图案共有棋子多少个?
”字形图案共有棋子多少个?
(4)计算前20个“![]() ”字形图案中棋子的总个数为______
”字形图案中棋子的总个数为______