题目内容
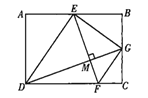
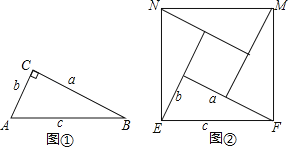
【题目】如图①，在Rt△ABC中∠C＝90°，两条直角边长分别为a，b，斜边长为c．如图②，现将与Rt△ABC全等的四个直角三角形拼成一个正方形EFMN．
（1）根据勾股定理的知识，请直接写出a，b，c之间的数量关系；
（2）若正方形EFMN的面积为64，Rt△ABC的周长为18，求Rt△ABC的面积．
【答案】（1）a2+b2＝c2；（2）9．
【解析】
（1）根据勾股定理得到a，b，c之间的数量关系；
（2）根据题意求出c，得到a+b的值，根据三角形的面积公式、完全平方公式计算，得到答案．
解：（1）由勾股定理得，a2+b2＝c2；
（2）∵正方形EFMN的面积为64，
∴c2＝64，即c＝8，
∵Rt△ABC的周长为18，
∴a+b+c＝18，
∴a+b＝10，
则Rt△ABC的面积＝
ab
＝
[（a+b）2﹣（a2+b2）]
＝9．
练习册系列答案
阅读快车系列答案
相关题目
