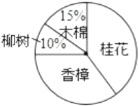
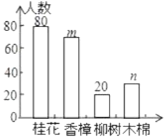
题目内容
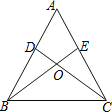
【题目】如图,点D、E分别为△ABC的边AB、AC上的点,BE与CD相交于点O,现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD,选择其中2个条件作为题设,余下2个条件作为结论,所有命题中,真命题的个数为( )
A. .3B. .4C. .5D. 、6
【答案】C
【解析】
本题实际是考查全等三角形的判定,根据条件可看出主要是围绕三角形ABE和ACD全等来求解的.已经有了一个公共角∠A,只要再知道一组对应角和一组对应边相等即可得出三角形全等的结论.
解:第一种:命题的条件是①和③,命题的结论是②和④.
∵AB=AC,∠ABE=∠ACD,∠BAC=∠CAB,
∴△ABE≌△ACD.
∴BE=CD.
又∠BCD=∠ACB﹣∠ACD=∠ABC﹣∠ABE=∠CBE,
∴△BOC是等腰三角形.
∴OB=OC;
同理可得:第二种:命题的条件是②和③,命题的结论是①和④.
第三种:命题的条件是①和②,命题的结论是③和④.
第四种:命题的条件是③和④,命题的结论是②和①.
第五种:命题的条件是②和④,命题的结论是①和③.
故选:C.

 阅读快车系列答案
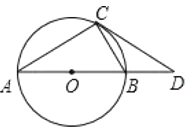
阅读快车系列答案【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
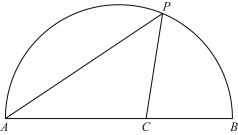
小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
【题目】太阳山中学九年级举行跳绳比赛,要求每班选出![]() 名学生参加,在规定时间内每人跳绳不低于
名学生参加,在规定时间内每人跳绳不低于![]() 次为优秀,冠、亚军会在甲、乙两班中产生,下表是这两个班的5名学生的比赛数据(单位:次)
次为优秀,冠、亚军会在甲、乙两班中产生,下表是这两个班的5名学生的比赛数据(单位:次)
|
|
|
|
| 平均次数 | 方差 | |
甲班 |
|
|
|
|
|
|
|
乙班 |
|
|
|
|
|
|
|
根据以上信息,解答下列问题:
(1)求出表中![]() 的值和甲、乙两班比赛学生的优秀率;
的值和甲、乙两班比赛学生的优秀率;
(2)求出两班的跳绳比赛数据的中位数;
(3)请你结合表格和自己所算出的数据判断冠军应发给哪个班?简要说明理由.