题目内容
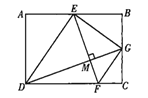
【题目】如图，点E是矩形ABCD的边AB的中点，点F是边CD上一点，连接ED，EF，ED平分∠AEF，过点D作DG⊥EF于点M，交BC于点G，连接GE，GF，若FG∥DE，则
的值是( )
A.
B.
C.
D.
【答案】C
【解析】
由题意得△AED≌△MED、△BEG≌△MEG、△MGF≌△CGF，设CG=x，用含x的式子表示AD =2x，
，即可得出
∵ED平分∠AEF
∴∠AED=∠DEM
在矩形ABCD中，∠A=∠B=∠BCD=90°
∵DG⊥EF
∴∠DME=∠EMG=∠GMF=90°
∴∠A=∠DME=90°
∵DE=DE
∴△AED≌△MED
∴ME=AE
∵点E是矩形ABCD的边AB的中点
∴AE=BE
∴ME=BE
∵∠EMC=∠B=90°， EG=EG
∴Rt△BEG≌Rt△MEG
∵AD∥BC
∴∠ADG=∠CGD
∵ED∥GF
∴∠EDM=∠FGM
∴∠ADE=∠CGF
∴∠CGF=∠FGM
∴△MGF≌△CGF
∴MG=CG=BG
设CG=x
∴BC=2x
∴AD=DM=2x
∴DG=3x
根据勾股定理可得
∴
∴
故选：C
练习册系列答案
口算能手系列答案
相关题目
