Question

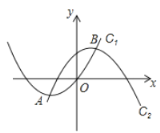
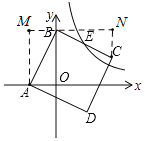
【题目】如图，正方形ABCD的点A，B点分别在x轴，y轴上，与双曲线y＝恰好交于BC的中点E，若OB＝2OA，则S△ABO的值为（ ）

A.6B.8C.12D.16

Answer 1

【答案】B

【解析】

过点B作x轴的平行线，过点A，C分别作y轴的平行线，两线相交于M，N，证明△ABM≌△BCN，可得BN＝AM＝2a，CN＝BM＝a，所以点C坐标为（2a，a），BC的中点E的坐标为（a，1.5a），把点E代入双曲线y＝，可得a的值，进而得出S△ABO的值．

解：如图，过点B作x轴的平行线，过点A，C分别作y轴的平行线，两线相交于M，N，

∵四边形ABCD为正方形，

∴∠ABC＝90°，AB＝BC，

∴∠ABM＝90°﹣∠CBN＝∠BCN，

∵∠M＝∠N＝90°，

∴△ABM≌△BCN（AAS），

∵OB＝2OA，

∴设OA＝a，OB＝2a，

则BN＝AM＝2a，CN＝BM＝a，

∴点C坐标为（2a，a），

∵E为BC的中点，B（0，2a），

∴E（a，1.5a），

把点E代入双曲线y＝，

得1.5a2＝12，a2＝8，

∴S△ABO＝＝8，

故选：B．