题目内容
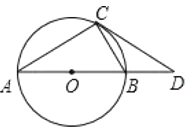
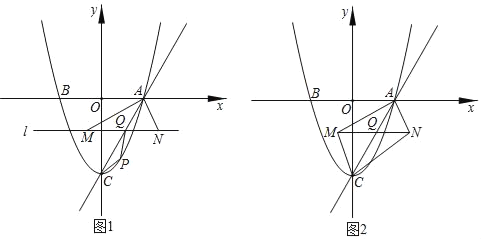
【题目】如图1,抛物线y=x2﹣3与x轴交于AB两点(点A在点B的右侧),与y轴交于点C,连接AC.点Q是线段AC上的动点,过Q作直线l∥x轴,直线1与∠BAC的平分线交于点M,与∠CAx的平分线交于点N.
(1)P是直线AC下方抛物线上一动点,连接PA,PC,当△PAC的面积最大时,求PQ+![]() AM的最小值;
AM的最小值;
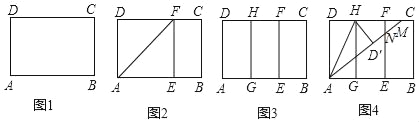
(2)如图2,连接MC,NC,当四边形AMCN为矩形时,将△AMN沿着直线AC平移得到△A'M'N',边A'M'所在的直线与y轴交于D点,若△DM'N'为等腰三角形时,求OD的长.
【答案】(1)![]() ;(2) OD的长为2或6或
;(2) OD的长为2或6或![]() .
.
【解析】
(1)用割补法求得△PAC面积的表达式,获得点P的坐标,利用30°构造AM为斜边的直角三角形,转换![]() AM的关系,可证点P到x轴的距离即为PQ+
AM的关系,可证点P到x轴的距离即为PQ+![]() AM的最小值;
AM的最小值;
(2)当四边形AMCN为矩形时,根据矩形的性质点Q为AC与MN的中点,△AMN的三边长度固定,当△DM'N'为等腰三角形时,以D、M'、N'为顶点分三类进行讨论,以线段相等作方程,求得OD的长.
解:(1)由已知可得![]()
设P(m,m2﹣3)
S△PAC=S△POC+S△AOP﹣S△AOC=![]()
当m=![]() 时,△PAC的面积有最大值,此时点P坐标
时,△PAC的面积有最大值,此时点P坐标![]()
如图,作AH⊥MN,
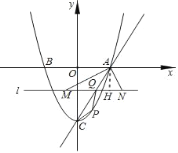
AH=![]() AM
AM
AH长为点Q到x轴的距离
PQ+![]() AM=PQ+AH=
AM=PQ+AH=![]()
(2)当四边形AMCN为矩形时,MN=AC,点Q为AC与MN中点
有题意可知,直线AC的解析式l1为y=![]() x﹣3
x﹣3
过点M与AC平行的直线解析式l2为y=![]() x
x
过点N与AC平行的直线解析式l3为y=![]() x﹣6
x﹣6
直线AM的解析式l4为![]()
设点N'(n,![]() n﹣6),M'(n﹣2
n﹣6),M'(n﹣2![]() ,
,![]() n﹣6)
n﹣6)
设直线A'M'的解析式为![]()
将点M'代入可得![]()
直线A'M'的解析式为![]()
则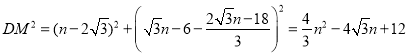
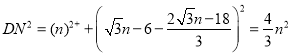
![]()
①当DM'=DN'时,DM'2=DN'2
![]()
解得n=![]()
OD=2
②当DM'=M'N'时,DM'2=M'N'2
![]()
解得n=0或3![]()
OD=6或0
③当DN'=M'N'时,DN'2=M'N'2
![]()
解得n=±3
OD=2![]()
综上所述,OD的长为2或6或2![]()

 名校课堂系列答案
名校课堂系列答案【题目】某工厂的甲、乙两个车间各生产了400个新款产品,为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围在165≤x<180为合格),分别从甲、乙两个车间生产的产品中随机各抽取了20个样品迸行检测,获得了它们的数据(尺寸),并对数据进行了整理、描述和分析.下面给出了部分信息:
a.甲车间产品尺寸的扇形统计图如下(数据分为6组:165≤x<170,170≤x<175,
175≤x<180,180≤x<185,185≤x<190,190≤x≤195):


b.甲车间生产的产品尺寸在175≤x<180这一组的是:
175 176 176 177 177 178 178 179 179
c.甲、乙两车间生产产品尺寸的平均数、中位数、众数如下:
车间 | 平均数 | 中位数 | 众数 |
甲车间 | 178 | m | 183 |
乙车间 | 177 | 182 | 184 |
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)此次检测中,甲、乙两车间生产的产品合格率更高的是 (填“甲”或“乙”),理由是 ;
(3)如果假设这个工厂生产的所有产品都参加了检测,那么估计甲车间生产该款新产品中合格产品有 个.