题目内容
【题目】如图,三角形ABC三边的长分别为AB=m2﹣n2,AC=2mn,BC=m2+n2,其中m、n都是正整数.以AB、AC、BC为边分别向外画正方形,面积分别为S1、S2、S3,那么S1、S2、S3之间的数量关系为_____.
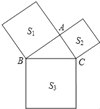
【答案】S1+S2=S3.
【解析】
首先利用勾股定理的逆定理判定△ABC是直角三角形,设Rt△ABC的三边分别为a、b、c,再分别用a、b、c表示S1、S2、S3的值,由勾股定理即可得出S1、S2、S3之间的数量关系.
解:∵AB=m2-n2,AC=2mn,BC=m2+n2,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
设Rt△ABC的三边分别为a、b、c,
∴S1=c2,S2=b2,S3=a2,
∵△ABC是直角三角形,
∴b2+c2=a2,即S1+S2=S3.
故答案为:S1+S2=S3.

练习册系列答案
相关题目