题目内容
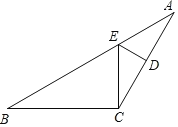
【题目】如图,抛物线![]() 经过点
经过点![]() ,点
,点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
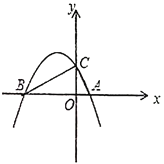
(1)求抛物线的解析式;
(2)点![]() 为抛物线第二象限上一点,满足
为抛物线第二象限上一点,满足![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,与抛物线交于另一点
,与抛物线交于另一点![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)将A,C坐标代入![]() 中解出即可;
中解出即可;
(2)由![]() 可得
可得![]() ,设
,设![]() ,利用三角形的面积求法建立方程求解即可得出结论;
,利用三角形的面积求法建立方程求解即可得出结论;
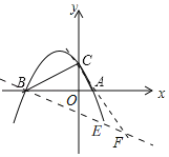
(3)延长AC与BE交于点F,易证△ABC是直角三角形可知△ACF是等腰直角三角形,由![]() ,
,![]() ,可得A是CF的中点,所以F(2,-2),进而确定直线BF的解析式为
,可得A是CF的中点,所以F(2,-2),进而确定直线BF的解析式为![]() ,即可求出E点坐标.
,即可求出E点坐标.
(1)将点![]() ,
,![]() 代入
代入![]() 得:
得:
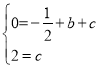
∴![]() ,
,![]() ,
,
∴![]() ;
;
(2)由(1)可得![]() ,
,
令y=0,解得![]() ,
,
则![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
如图,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,
,
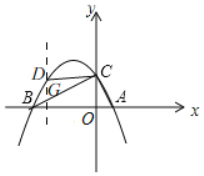
设![]() ,
,
∴![]()
∴![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ;
;
(3)延长![]() 与
与![]() 交于点
交于点![]() ,
,![]() 是直角三角形,
是直角三角形,
∵直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∵![]() ,
,![]() ,
,
∴![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
则![]()
![]()
![]()
![]()
![]() ,
,
∴![]() 或
或![]() ,
,
∵![]() 与
与![]() 重合舍去,
重合舍去,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目