جâؤ؟ؤعبف
،¾جâؤ؟،؟بçح¼¢ظ£¬،÷ABCضذ£¬،دABC=45،م£¬AH،حBCسعµمH£¬µمDشعAHةد£¬ازDH=CH£¬ء¬½لBD£®
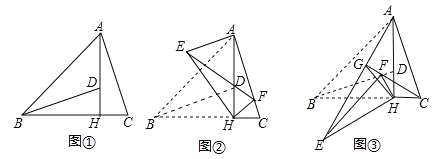
£¨1£©اَض¤£؛BD=AC£»
£¨2£©½«،÷BHDبئµمHذ×ھ£¬µأµ½،÷EHF£¨µمB£¬D·ض±ًسëµمE£¬F¶شس¦£©£¬ء¬½سAE£®
¢ظبçح¼¢ع£¬µ±µمFآنشعACةدت±£¬£¨F²»سëCضط؛د£©£¬بôBC=4£¬tanC=3£¬اَAEµؤ³¤£»
¢عبçح¼¢غ£¬µ±،÷EHFتاسة،÷BHDبئµمHؤوت±صëذ×ھ30،مµأµ½ت±£¬ةèةندكCFسëAEدཻسعµمG£¬ء¬½سGH£¬تشج½¾؟دك¶خGHسëEFض®¼نآْ×مµؤµبء؟¹طدµ£¬²¢ثµأ÷ہيسة£®
،¾´ً°¸،؟£¨1£©ض¤أ÷¼û½âخِ£»£¨2£©¢ظ![]() £»¢ع
£»¢ع![]() £½
£½![]() £®
£®
،¾½âخِ،؟
تشجâ·ضخِ£؛£¨1£©دبإذ¶د³ِAH=BH£¬شظإذ¶د³ِ،÷BHD،ص،÷AHC¼´؟ة£»
£¨2£©¢ظدب¸ù¾فtanC=3£¬اَ³ِAH=3£¬CH=1£¬ب»؛َ¸ù¾ف،÷EHA،ص،÷FHC£¬µأµ½£¬HP=3AP£¬AE=2AP£¬×î؛َسأ¹´¹ة¶¨ہي¼´؟ة£»
¢عدبإذ¶د³ِ،÷AGQ،×،÷CHQ£¬µأµ½![]() £¬ب»؛َإذ¶د³ِ،÷AQC،×،÷GQH£¬سأدàثئ±ب¼´؟ة£®
£¬ب»؛َإذ¶د³ِ،÷AQC،×،÷GQH£¬سأدàثئ±ب¼´؟ة£®
تشجâ½âخِ£؛£¨1£©شعRt،÷AHBضذ£¬،دABC=45،م£¬،àAH=BH£¬شع،÷BHD؛ح،÷AHCضذ£¬،كAH=BH£¬،دBHD=،دAHC£¬DH=CH£¬،à،÷BHD،ص،÷AHC£¬،àBD=AC£»
£¨2£©¢ظبçح¼£¬شعRt،÷AHCضذ£¬،كtanC=3£¬،à![]() =3£¬ةèCH=x£¬،àBH=AH=3x£¬،كBC=4£¬،à3x+x=4£¬،àx=1£¬،àAH=3£¬CH=1£¬سةذ×ھضھ£¬،دEHF=،دBHD=،دAHC=90،م£¬EH=AH=3£¬CH=DH=FH£¬،à،دEHA=،دFHC£¬
=3£¬ةèCH=x£¬،àBH=AH=3x£¬،كBC=4£¬،à3x+x=4£¬،àx=1£¬،àAH=3£¬CH=1£¬سةذ×ھضھ£¬،دEHF=،دBHD=،دAHC=90،م£¬EH=AH=3£¬CH=DH=FH£¬،à،دEHA=،دFHC£¬![]() £¬،à،÷EHA،ص،÷FHC£¬،à،دEAH=،دC£¬،àtan،دEAH=tanC=3£¬¹µمH×÷HP،حAE£¬،àHP=3AP£¬AE=2AP£¬شعRt،÷AHPضذ£¬
£¬،à،÷EHA،ص،÷FHC£¬،à،دEAH=،دC£¬،àtan،دEAH=tanC=3£¬¹µمH×÷HP،حAE£¬،àHP=3AP£¬AE=2AP£¬شعRt،÷AHPضذ£¬![]() £¬،à
£¬،à![]() £¬،àAP=
£¬،àAP=![]() £¬،àAE=
£¬،àAE=![]() £»
£»
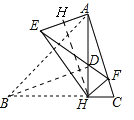
¢عسة¢ظسذ£¬،÷AEH؛ح،÷FHC¶¼خھµبرüب½اذخ£¬،à،دGAH=،دHCG=90،م£¬،à،÷AGQ،×،÷CHQ£¬،à![]() £¬،à
£¬،à![]() £¬،ك،دAQC=،دGQE£¬،à،÷AQC،×،÷GQH£¬،à
£¬،ك،دAQC=،دGQE£¬،à،÷AQC،×،÷GQH£¬،à![]() =sin30،م=
=sin30،م=![]() £®
£®