题目内容
【题目】如图,四边形ABCD,AD∥BC,∠B=90,AD=6,AB=4,BC=9.
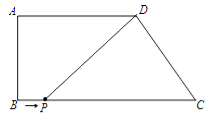
(1)求CD的长为.
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?
【答案】(1)5(2)①PD=DC, t=3 ②PC=DC, t=5 ③PD=PC, t=65/18
【解析】
试题分析:(1)过点D作![]() ,垂足为
,垂足为![]() ,先判断出四边形
,先判断出四边形![]() 是矩形,在
是矩形,在![]() 中根据勾股定理即可得出
中根据勾股定理即可得出![]() 的长;
的长;
(2) 过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由题意得
,由题意得![]() ,
,![]() .再分
.再分![]() ,
,![]() ,
,![]() 三种情况进行讨论.
三种情况进行讨论.
试题解析:
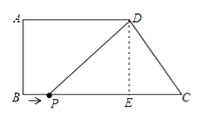
(1)过点D作![]() ,垂足为E,
,垂足为E,
∵![]() ,
,![]() ,
,
∴四边形ABED是矩形,
∴BE=AD=6,DE=AB=4,
∴CE=BC﹣BE=9﹣6=3,
在Rt△DCE中,![]() .
.
故答案为:5;
(2)过点D作DE⊥BC,垂足为E,由题意得PC=9﹣t,PE=6﹣t.
当CD=CP时,5=9﹣t,解得t=4;
当CD=PD时,E为PC中点,
∴6﹣t=3,
∴t=3;
当PD=PC时,![]() ,
,
∴![]() ,
,
解得t= ![]() .
.
故t的值为t=3或4或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目