题目内容
【题目】如图,△ABC中,AB=AC,∠A=36°,称满足此条件的三角形为黄金等腰三角形.请完成以下操作:(画图不要求使用圆规,以下问题所指的等腰三角形个数均不包括△ABC)
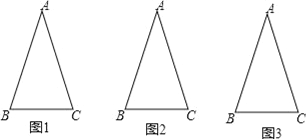
(1)在图1中画1条线段,使图中有2个等腰三角形,并直接写出这2个等腰三角形的顶角度数分别是 度和 度;
(2)在图2中画2条线段,使图中有4个等腰三角形;
(3)继续按以上操作发现:在△ABC中画n条线段,则图中有 个等腰三角形,其中有 个黄金等腰三角形.
【答案】(1)108,36;(2)作图见解析;(3)2n,n.
【解析】试题分析:(1)利用等腰三角形的性质以及∠A的度数,进而得出这2个等腰三角形的顶角度数;
(2)利用(1)种思路进而得出符合题意的图形;
(3)利用当1条直线可得到2个等腰三角形;当2条直线可得到4个等腰三角形;当3条直线可得到6个等腰三角形,进而得出规律求出答案.
试题解析:(1)如图1所示:∵AB=AC,∠A=36°,
∴当AE=BE,则∠A=∠ABE=36°,则∠AEB=108°,
则∠EBC=36°,
∴这2个等腰三角形的顶角度数分别是108度和36度;
故答案为:108,36;
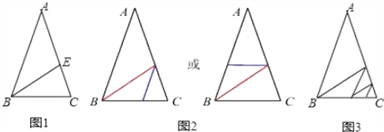
(2)如图2所示:
(3)如图3所示:当1条直线可得到2个等腰三角形;
当2条直线可得到4个等腰三角形;
当3条直线可得到6个等腰三角形;
…
∴在△ABC中画n条线段,则图中有2n个等腰三角形,其中有n个黄金等腰三角形.
故答案为:2n,n.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目