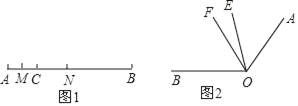��Ŀ����
����Ŀ����֪��A��B�������϶�Ӧ�����ֱ�Ϊa��b����|a��4|��(b��2)2��0����A��B֮��ľ������AB.
(1)�߶�AB�ij�Ϊ ��(ֱ��д�����)
(2)������P�������϶�Ӧ����Ϊx.
�ٵ�PA��PB��ֵ��Сʱ��������x��ֵΪ ��(ֱ��д�����)
�ڵ�PA��PB��14ʱ����x��ֵ��
(3)������P�ڵ�A����࣬M��N�ֱ���PA��PB���е㣬����P��A������ƶ�ʱ��������С��ͬѧ�ڼ���PM��PN��PN��PM��ֵʱ���֣�����ֻ��һ����ֵ�Dz���ģ������жϳ���һ����ֵ���䣬�������ֵ��
���𰸡���1��6��2���٣�3����1,1����x��ֵΪ��8��6��3��PN��PM��3
��������
��1�����ݷǸ������������a��b��ֵ���ɽ�����⣻
��2���ٵ�PA+PB��ֵ��Сʱ����ʾ��x�ĵ�P���߶�AB�ϣ��ɴ˼��ɽ�����⣻
�ڷ����������г�������⼴�ɣ�
��3��PN-PM��ֵ���䣮�г�PN��PM�Ĵ���ʽ���ɽ�����⣻
�⣺��1����|a+4|+��b-2��2=0��
�֡�|a+4|��0����b-2��2��0��
��a=-4��b=2��
��AB=2-��-4��=6��
�ʴ�Ϊ6��
��2���ٵ�PA+PB��ֵ��Сʱ��������x��ֵΪ-3��-1��1��
�ʴ�Ϊ-3��-1��1��
�ڵ���P�ڵ�A���ʱ��2-x+-4-x=14�����x=-8��
����P�ڵ�B�ұ�ʱ��x-2+x+4=14�����x=6��
��x��ֵΪ-8��6��
��3�����ۣ�PN-PM��ֵ���䣮
���ɣ���PN=![]() ��2-x����PM=
��2-x����PM=![]() ��-4-x����
��-4-x����
��PN-PM=1-![]() x+2+
x+2+![]() x=3��
x=3��
��PN-PM��ֵ���䣬���ֵΪ3��

 Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д� ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣬Ϊ�˴������㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3000��ѧ���μӵġ�������д�����������������в���ѧ���ijɼ���������50�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������200��ѧ���ijɼ����ɼ�xȡ�������ܷ�100�֣���Ϊ���������������õ����в�������ͳ��ͼ����
�ɼ�x/�� | Ƶ�� | Ƶ�� |
50��x��60 | 10 | 0.05 |
60��x��70 | 30 | 0.15 |
70��x��80 | 40 | n |
80��x��90 | m | 0.35 |
90��x��100 | 50 | 0.25 |
�����������Ϣ������������⣺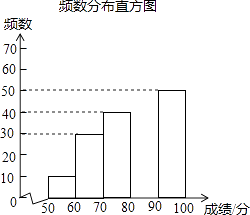
��1��m= �� n=��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����α����ɼ�����λ�������������Σ�
��4�����ɼ���90�����ϣ�����90�֣���Ϊ���š��ȣ����У�μ���α�����3000��ѧ���гɼ����š���Լ�ж����ˣ�