题目内容
【题目】如图,AE是半圆O的直径,弦AB=BC=2 ![]() ,弦CD=DE=2,连结OB,OD,求图中两个阴影部分的面积和.
,弦CD=DE=2,连结OB,OD,求图中两个阴影部分的面积和. 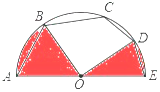
【答案】解:∵弦AB=BC,弦CD=DE, ∴点B是弧AC的中点,点D是弧CE的中点,
∴∠BOD=90°,
过点O作OF⊥BC于点F,OG⊥CD于点G.
则BF=FC= ![]() ,CG=GD=1,∠FOG=45°,
,CG=GD=1,∠FOG=45°,
在四边形OFCG中,∠FCD=135°,
过点C作CN∥OF,交OG于点N,
则∠FCN=90°,∠NCG=135°﹣90°=45°,
∴△CNG为等腰三角形,
∴CG=NG=1,
过点N作NM⊥OF于点M,则MN=FC= ![]() ,
,
在等腰三角形MNO中,NO= ![]() MN=2,
MN=2,
∴OG=ON+NG=3,
在Rt△OGD中,OD= ![]() =
= ![]() =
= ![]() ,
,
即圆O的半径为 ![]() ,
,
故S阴影=S扇形OBD= 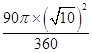 =
= ![]() π.
π.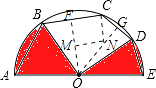
【解析】根据弦AB=BC,弦CD=DE,可得∠BOD=90°,∠BOD=90°,过点O作OF⊥BC于点F,OG⊥CD于点G,在四边形OFCG中可得∠FCD=135°,过点C作CN∥OF,交OG于点N,判断△CNG、△OMN为等腰直角三角形,分别求出NG、ON,继而得出OG,在Rt△OGD中求出OD,即得圆O的半径,代入扇形面积公式求解即可.
【考点精析】本题主要考查了扇形面积计算公式的相关知识点,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.

【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”某校本学年开展了读书活动,在这次活动中,八年级![]() 班40名学生读书册数的情况如表
班40名学生读书册数的情况如表
读书册数 | 4 | 5 | 6 | 7 | 8 |
人数 | 6 | 4 | 10 | 12 | 8 |
根据表中的数据,求:
(1)该班学生读书册数的平均数;
(2)该班学生读书册数的中位数.