题目内容
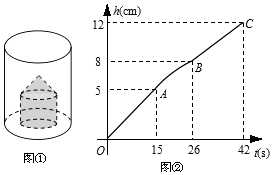
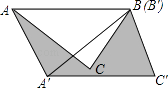
【题目】如图,AD、![]() 分别是锐角三角形ABC和锐角三角形
分别是锐角三角形ABC和锐角三角形![]() 中BC、
中BC、![]() 边上的高,且
边上的高,且![]() 、
、![]() .若使△ABC≌△
.若使△ABC≌△![]() ,请你补充条件_________.(填写一个你认为适当的条件即可)
,请你补充条件_________.(填写一个你认为适当的条件即可)

【答案】∠BAC=∠B′A′C′或∠C=∠C′或BC=B′C′(答案不唯一)
【解析】
已知AB=A′B′,A′D′=AD;根据斜边直角边定理即可证得Rt△ABD≌Rt△A'B'D',由此可得出∠B=∠B',因此△ABC和△A'B'C'中,已知了AB=A'B',∠B=∠B',只需再添加一组对应角相等或BC=B'C'即可证得两三角形全等.
∵AB=A′B′,A′D′=AD,
∴Rt△ABD≌Rt△A′B′D′(HL);
∴∠B=∠B′,
又∵AB=A′B′,
∴当∠BAC=∠B′A′C′或∠C=∠C′或BC=B′C′时,△ABC≌△A′B′C′.
故答案为:∠BAC=∠B′A′C′或∠C=∠C′或BC=B′C′.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”某校本学年开展了读书活动,在这次活动中,八年级![]() 班40名学生读书册数的情况如表
班40名学生读书册数的情况如表
读书册数 | 4 | 5 | 6 | 7 | 8 |
人数 | 6 | 4 | 10 | 12 | 8 |
根据表中的数据,求:
(1)该班学生读书册数的平均数;
(2)该班学生读书册数的中位数.