题目内容
【题目】如图,在射线OM上有三点A,B,C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O出发,沿OM方向以1cm/s的速度运动,点Q从点C出发在线段CO上向点O匀速运动(点Q运动到点O时停止运动),两点同时出发.
(1)当PA=2PB(P在线段AB上)时,点Q运动到的位置恰好是线段AB的中点,求点Q的运动速度;
(2)若点Q的运动速度为3cm/s,经过多长时间P,Q两点相距70cm?
(3)当点P运动到线段AB上时,分别取OP和AB的中点E,F,求![]() .
.
![]()
【答案】(1)点Q的运动速度为![]() cm/s;(2)经过5秒或70秒两点相距70cm;(3)
cm/s;(2)经过5秒或70秒两点相距70cm;(3)![]() .
.
【解析】
(1)根据![]() ,求得
,求得![]() ,得到
,得到![]() ,求得
,求得![]() ,根据线段中点的定义得到
,根据线段中点的定义得到![]() ,求得
,求得![]() ,由此即得到结论;
,由此即得到结论;
(2)分点P、Q相向而行和点P、Q直背而行两种情况,设运动时间为t秒,然后分别根据线段的和差、速度公式列出等式求解即可得;
(3)先画出图形,再根据线段的和差、线段的中点定义求出![]() 和EF的长,从而即可得出答案.
和EF的长,从而即可得出答案.
(1)∵点P在线段AB上时,![]()
∴![]()
∴![]()
∴![]()
∵点Q是线段AB的中点
∴![]()
∴![]()
∴点Q的运动速度为![]() ;
;
(2)设运动时间为t秒
则![]()
∵点Q运动到O点时停止运动
∴点Q最多运动时间为![]()
依题意,分以下两种情况:
①当点P、Q相向而行时
![]() ,即
,即![]()
解得![]()
②当点P、Q直背而行时
若![]() ,则
,则![]()
![]()
因此,点Q运动![]() 到点O停止运动后,点P继续运动
到点O停止运动后,点P继续运动![]() ,点P、Q相距正好等于
,点P、Q相距正好等于![]() ,此时运动时间为
,此时运动时间为![]()
综上,经过5秒或70秒,P、Q两点相距![]() ;
;
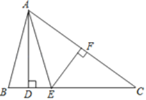
(3)如图,设![]()
点P在线段AB上,则![]() ,即
,即![]()
![]()
![]() 点E、F分别为OP和AB的中点
点E、F分别为OP和AB的中点
![]()
![]()
![]()
则 .
.
![]()

 名校课堂系列答案
名校课堂系列答案【题目】已知甲、乙两袋中各装有若干颗球,其种类与数量如表所示.今阿冯打算从甲袋中抽出一颗球,小潘打算从乙袋中抽出一颗球,若甲袋中每颗球被抽出的机会相等,且乙袋中每颗球被抽出的机会相等,则下列叙述何者正确?( )
甲袋 | 乙袋 | |
红球 | 2颗 | 4颗 |
黄球 | 2颗 | 2颗 |
绿球 | 1颗 | 4颗 |
总计 | 5颗 | 10颗 |
A. 阿冯抽出红球的机率比小潘抽出红球的机率大
B. 阿冯抽出红球的机率比小潘抽出红球的机率小
C. 阿冯抽出黄球的机率比小潘抽出黄球的机率大
D. 阿冯抽出黄球的机率比小潘抽出黄球的机率小