题目内容
【题目】如图,以AB为直径的⊙O的圆心O到直线l的距离OE=3,⊙O的半径r=2,直线AB不垂直于直线l,过点A,B分别作直线l的垂线,垂足分别为点D,C,则四边形ABCD的面积的最大值为__________.
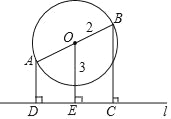
【答案】12
【解析】先判断OE为直角梯形ADCB的中位线,则OE=![]() (AD+BC),所以S四边形ABCD=OECD=3CD,只有当CD=AB=4时,CD最大,从而得到S四边形ABCD最大值.
(AD+BC),所以S四边形ABCD=OECD=3CD,只有当CD=AB=4时,CD最大,从而得到S四边形ABCD最大值.
∵OE⊥l,AD⊥l,BC⊥l,
而OA=OB,
∴OE为直角梯形ADCB的中位线,
∴OE=![]() (AD+BC),
(AD+BC),
∴S四边形ABCD=![]() (AD+BC)CD=OECD=3CD,
(AD+BC)CD=OECD=3CD,
当CD=AB=4时,CD最大,S四边形ABCD最大,最大值为12.

练习册系列答案
相关题目
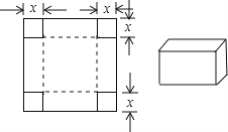
【题目】如图所示,一张边长为16cm的正方形硬纸板,把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
(1)用含有x的代数式表示V,则V=______;
(2)完成下表:
x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
V(cm2) |
(3)观察上表,容积V的值是否随x的增大而增大?当x取什么值时,容积V的值最大?