题目内容
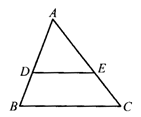
如图,在正三角形 中,
中, ,
, ,
, 分别是
分别是 ,
, ,
, 上的点,
上的点, ,
, ,
, ,则
,则 的面积与
的面积与 的面积之比等于 .
的面积之比等于 .
 中,
中, ,
, ,
, 分别是
分别是 ,
, ,
, 上的点,
上的点, ,
, ,
, ,则
,则 的面积与
的面积与 的面积之比等于 .
的面积之比等于 .
1:3
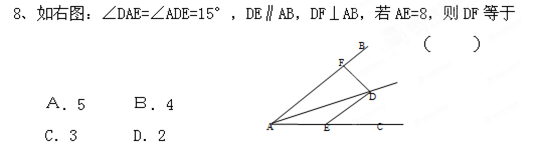
分析:首先根据题意求得:∠DFE=∠FED=∠EDF=60°,即可证得△DEF是正三角形,又由直角三角形中,30°所对的直角边是斜边的一半,得到边的关系,即可求得DF:AB=1: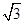
,又由相似三角形的面积比等于相似比的平方,即可求得结果.
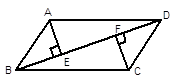
解答:解:∵△ABC是正三角形,
∴∠B=∠C=∠A=60°,
∵DE⊥AC,EF⊥AB,FD⊥BC,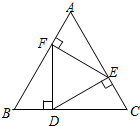
∴∠AFE=∠CED=∠BDF=90°,
∴∠BFD=∠CDE=∠AEF=30°,
∴∠DFE=∠FED=∠EDF=60°,
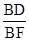 =
=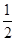 ,
,
∴△DEF是正三角形,
∴BD:DF=1: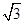 ①,
①,
BD:AB=1:3②,
△DEF∽△ABC,
①÷②,
 =
=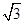 ,
,
∴DF:AB=1: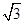 ,
,
∴△DEF的面积与△ABC的面积之比等于1:3.
故答案为:1:3.
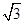
,又由相似三角形的面积比等于相似比的平方,即可求得结果.
解答:解:∵△ABC是正三角形,
∴∠B=∠C=∠A=60°,
∵DE⊥AC,EF⊥AB,FD⊥BC,

∴∠AFE=∠CED=∠BDF=90°,
∴∠BFD=∠CDE=∠AEF=30°,
∴∠DFE=∠FED=∠EDF=60°,
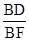 =
=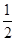 ,
,∴△DEF是正三角形,
∴BD:DF=1:
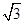 ①,
①,BD:AB=1:3②,
△DEF∽△ABC,
①÷②,
 =
=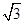 ,
,∴DF:AB=1:
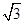 ,
,∴△DEF的面积与△ABC的面积之比等于1:3.
故答案为:1:3.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
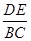 的值小题2: (2)求
的值小题2: (2)求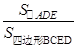 的值
的值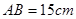 ,
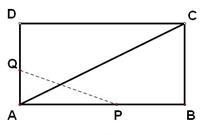
,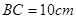 ,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动。如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与
,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动。如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与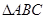 相似?
相似?