题目内容
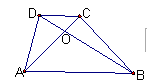
在平行四边形ABCD中,E、F是对角线BD上的点,且BE=EF=FD,连接AE交BC于点M,连接MF交AD于点H,则△AMH和平行四边形ABCD的面积比为
3:8
分析:由平行四边形的性质及平行线的性质求出AH:AD的值,再根据△AMH与?ABCD等高,利用面积公式求底边的比.
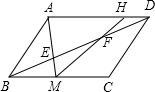
解:∵BE=EF=FD,
∴DE=2BE,BF=2DF,
∵AD∥BC,
∴△ADE∽△MBE,△BMF∽△DHF,
∴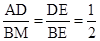 ,即BM=
,即BM=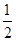 AD,
AD,
同理可得DH=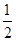 BM=
BM=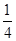 AD,
AD,
∴AH=AD-DH=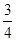 AD,
AD,
设△AMH的AH边上高为h,
则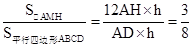 .
.
故答案为:3:8.

解:∵BE=EF=FD,
∴DE=2BE,BF=2DF,
∵AD∥BC,
∴△ADE∽△MBE,△BMF∽△DHF,
∴
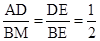 ,即BM=
,即BM=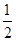 AD,
AD,同理可得DH=
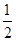 BM=
BM=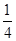 AD,
AD,∴AH=AD-DH=
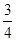 AD,
AD,设△AMH的AH边上高为h,
则
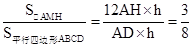 .
.故答案为:3:8.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
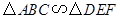 ,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为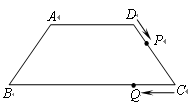
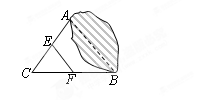
 ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2. E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设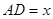 ,
,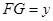 ,
,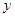 关于
关于 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域; 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,
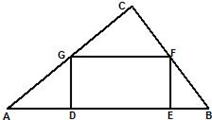
 中,
中, ,
, ,
,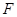 分别是
分别是 ,
, ,
,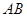 上的点,
上的点,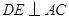 ,
,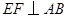 ,
,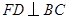 ,则
,则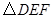 的面积与
的面积与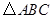 的面积之比等于 .
的面积之比等于 .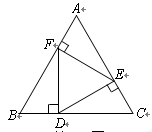
 两处被池塘隔开,为了测量
两处被池塘隔开,为了测量 外选一适当的点
外选一适当的点 ,连接
,连接 ,并分别取线段
,并分别取线段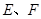 ,测得
,测得 =20m,则
=20m,则