题目内容
【题目】三角形的下列四种线段中一定能将三角形分成面积相等的两部分的是( )
A.角平分线
B.中位线
C.高
D.中线
【答案】D
【解析】解:( 1 ) 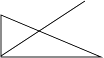 三角形的角平分线把三角形分成两部分,这两部分的面积比分情况而定;
三角形的角平分线把三角形分成两部分,这两部分的面积比分情况而定;
( 2 ) 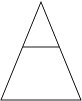
三角形的中位线把三角形分成两部分,这两部分的面积经计算得:
三角形面积为梯形面积的;
( 3 ) 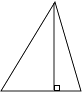
三角形的高把三角形分成两部分,这两部分的面积比分情况而定;
( 4 ) 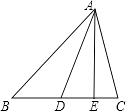
三角形的中线AD把三角形分成两部分,△ABD的面积为BDAE,△ACD面积为CDAE;因为AD为中线,所以D为BC中点,所以BD=CD,所以△ABD的面积等于△ACD的面积。
∴三角形的中线把三角形分成面积相等的两部分。
所以答案是:D。
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目