Question

【题目】在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．

（一）尝试探究

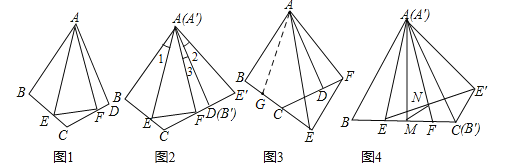
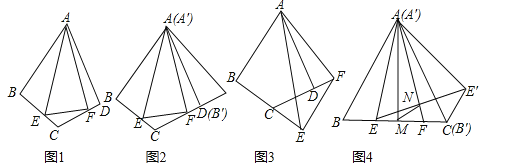
如图1，在四边形ABCD中，AB=AD，∠BAD=60°，∠ABC=∠ADC=90°，点E、F分别在线段BC、CD上，∠EAF=30°，连接EF．

（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF= 度，线段BE、EF、FD之间的数量关系为 ．

（2）如图3，当但点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．

（二）拓展延伸

如图4，在等边△ABC中，E、F是边BC上的两点，∠EAF=30°，BE=1，将△ABE绕点A逆时针旋转60°得到△A′B′E′（A′B′与AC重合），连接EE′，AF与EE′交于点N，过点A作AM⊥BC于点M，连接MN，求线段MN的长度．

Answer 1

【答案】（一）（1）30，BE+DF=EF；（2）BE﹣DF=EF；（二）．

【解析】

试题分析：（一）（1）根据图形旋转前后对应边相等，对应角相等，判定△AEF≌△AE′F，进而根据线段的和差关系得出结论；

（2）先在BE上截取BG=DF，连接AG，构造△ABG≌△ADF，进而利用全等三角形的对应边相等，对应角相等，判定△GAE≌△FAE，最后根据线段的和差关系得出结论；

（二）先根据旋转的性质判定△AEE′是等边三角形，进而利用等边△ABC、等边△AEE′的三线合一的性质，得到和∠BAE=∠MAN，最后判定△BAE∽△MAN，并根据相似三角形对应边成比例，列出比例式求得MN的长．

试题解析：（一）（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′，则

∠1=∠2，BE=DE′，AE=AE′，∵∠BAD=60°，∠EAF=30°，∴∠1+∠3=30°，∴∠2+∠3=30°，即∠FAE′=30°，∴∠EAF=∠FAE′，在△AEF和△AE′F中，∵AE=AE′，∠EAF=∠FAE′，AF=AF，∴△AEF≌△AE′F（SAS），∴EF=E′F，即EF=DF+DE′，∴EF=DF+BE，即线段BE、EF、FD之间的数量关系为BE+DF=EF，故答案为：30，BE+DF=EF；

（2）如图3，在BE上截取BG=DF，连接AG，在△ABG和△ADF中，∵AB=AD，∠ABE=∠ADF，BG=DF，∴△ABG≌△ADF（SAS），∴∠BAG=∠DAF，且AG=AF，∵∠DAF+∠DAE=30°，∴∠BAG+∠DAE=30°，∵∠BAD=60°，∴∠GAE=60°﹣30°=30°，∴∠GAE=∠FAE，在△GAE和△FAE中，∵AG=AF，∠GAE=∠FAE，AE=AE，∴△GAE≌△FAE（SAS），∴GE=FE，又∵BE﹣BG=GE，BG=DF，∴BE﹣DF=EF，即线段BE、EF、FD之间的数量关系为BE﹣DF=EF；

（二）如图4，将△ABE绕点A逆时针旋转60°得到△A′B′E′，则

AE=AE′，∠EAE′=60°，∴△AEE′是等边三角形，又∵∠EAF=30°，∴AN平分∠EAF，∴AN⊥EE′，∴直角三角形ANE中，=，∵在等边△ABC中，AM⊥BC，∴∠BAM=30°，∴=，且∠BAE+∠EAM=30°，∴，又∵∠MAN+∠EAM=30°，∴∠BAE=∠MAN，∴△BAE∽△MAN，∴，即=，∴MN=．