��Ŀ����
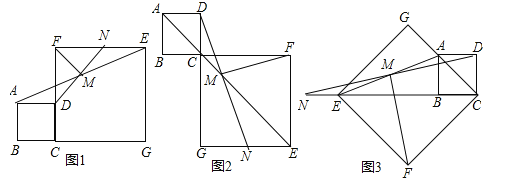
����Ŀ����ͼ1��ʾ����������ABCD��������CGEF�У���B��C��G��ͬһ��ֱ���ϣ�M���߶�AE���е㣬DM���ӳ��߽�EF�ڵ�N������FM����֤��DM=FM��DM��FM������д֤�����̣�
��1����ͼ2������B��C��F��ͬһ��ֱ���ϣ�DM���ӳ��߽�EG�ڵ�N�������������䣬��̽���߶�DM��FM�������Ĺ�ϵ����д�����룬������֤����
��2����ͼ3������E��B��C��ͬһ��ֱ���ϣ�DM���ӳ��߽�CE���ӳ����ڵ�N�������������䣬̽���߶�DM��FM�������Ĺ�ϵ����ֱ��д�����룮
���𰸡���1��DM=FM��DM��FM��֤���������������2��DM=FM��DM��FM��
��������
�����������1������DF��NF�������������������õ�AD��BC��BC��GE��������AD��GE���õ���DAM=��NEM������֤����MAD�ա�MEN���ó�DM=MN��AD=EN���Ƴ���MAD�ա�MEN����DFN�ǵ���ֱ�������Σ����ɵõ����ۣ�
��2������DF��NF�������������������õ�AD��BC��AD��CN�������õ���DAM=��NEM����֤��MAD�ա�MEN����DM=MN��AD=EN���Ƴ���MAD�ա�MEN����DFN�ǵ���ֱ�������Σ��������õ����ۣ�
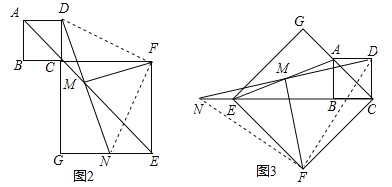
�����������1����ͼ2��DM=FM��DM��FM��֤�����£�
����DF��NF�����ı���ABCD��CGEF�������Σ���AD��BC��BC��GE����AD��GE�����DAM=��NEM����M��AE���е㣬��AM=EM������MAD����MEN�У��ߡ�AMD=��EMN��AM=EM����DAM=��NEM�����MAD�ա�MEN����DM=MN��AD=EN����AD=CD����CD=NE����CF=EF����DCF=��DCB=90�㣬����DCF����NEF�У���CD=EN����DCF=��NEF=90����CF=EF�����MAD�ա�MEN����DF=NF����CFD=��EFN���ߡ�EFN+��NFC=90�㣬���DFC+��CFN=90�㣬���DFN=90�㣬��DM��FM��DM=FM��
��2�����룺DM��FM��DM=FM��
֤�����£���ͼ3������DF��NF�����ı���ABCD�������Σ���AD��BC������E��B��C��ͬһ��ֱ���ϣ���AD��CN�����ADN=��MNE������MAD����MEN�У��ߡ�AMD=��EMN��AM=EM����DAM=��NEM�����MAD�ա�MEN����DM=MN��AD=EN����AD=CD����CD=NE����CF=EF���ߡ�DCF=90��+45��=135�㣬��NEF=180�㩁45��=135�㣬���DCF=��NEF������DCF����NEF�У���CD=NE����DCF=��NEF=135����CF=EF�����MAD�ա�MEN����DF=NF����CFD=��EFN���ߡ�CFD+��EFD=90�㣬���NFE+��EFD=90�㣬���DFN=90�㣬��DM��FM��DM=FM��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�