题目内容
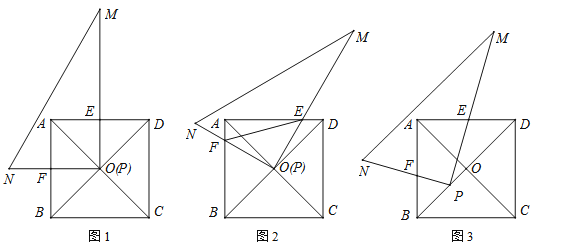
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系.
【答案】(1)PE=PF;(2)①成立;②![]() ;③PE=2PF,PE=(m﹣1)PF.
;③PE=2PF,PE=(m﹣1)PF.
【解析】
试题分析:(1)由正方形的性质和角平分线的性质解答即可;
(2)①由正方形的性质和旋转的性质证明△FOA≌△EOD,即可得到答案;
②作OG⊥AB于G,由余弦的概念求出OF的长,由勾股定理求值即可;
③过点P作HP⊥BD交AB于点H,由相似三角形的判定和性质求出PE与PF的数量关系,由解答结果总结规律得到当BD=mBP时,PE与PF的数量关系.
试题解析:(1)PE=PF,理由:∵四边形ABCD为正方形,∴∠BAC=∠DAC,又PM⊥AD、PN⊥AB,∴PE=PF;
(2)①成立,理由:∵AC、BD是正方形ABCD的对角线,∴OA=OD,∠FAO=∠EDO=45°,∠AOD=90°,∴∠DOE+∠AOE=90°,∵∠MPN=90°,∴∠FOA+∠AOE=90°,∴∠FOA=∠DOE,在△FOA和△EOD中,∵∠FAO=∠FDO,OA=OD,∠FOA=∠DOE,∴△FOA≌△EOD,∴OE=OF,即PE=PF;
②作OG⊥AB于G,∵∠DOM=15°,∴∠AOF=15°,则∠FOG=30°,∵cos∠FOG=![]() ,∴OF=
,∴OF=![]() =
=![]() ,又OE=OF,∴EF=
,又OE=OF,∴EF=![]() ;
;
③PE=2PF,如图3,过点P作HP⊥BD交AB于点H,则△HPB为等腰直角三角形,∠HPD=90°,∴HP=BP,∵BD=3BP,∴PD=2BP,∴PD=2 HP,又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°,∴∠HPF=∠DPE,又∵∠BHP=∠EDP=45°,∴△PHF∽△PDE,∴![]() ,即PE=2PF,由此规律可知,当BD=mBP时,PE=(m﹣1)PF.
,即PE=2PF,由此规律可知,当BD=mBP时,PE=(m﹣1)PF.


 巧学巧练系列答案
巧学巧练系列答案