题目内容
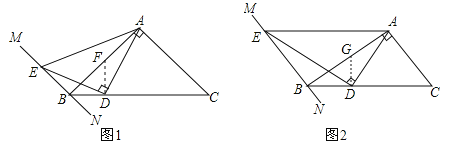
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)

【答案】(1)证明见试题解析;(2)DE=![]() AD;(3)AD=DEtanα.
AD;(3)AD=DEtanα.
【解析】
试题分析:(1)过点D作DF⊥BC,交AB于点F,得出∠BDE=∠ADF,∠EBD=∠AFD,即可得到△BDE≌△FDA,从而得到AD=DE;
(2)过点D作DG⊥BC,交AB于点G,进而得出∠EBD=∠AGD,证出△BDE∽△GDA即可得出答案;
(3)过点D作DG⊥BC,交AB于点G,进而得出∠EBD=∠AGD,证出△BDE∽△GDA即可得出答案.
试题解析:(1)如图1,过点D作DF⊥BC,交AB于点F,则∠BDE+∠FDE=90°,∵DE⊥AD,∴∠FDE+∠ADF=90°,∴∠BDE=∠ADF,∵∠BAC=90°,∠ABC=45°,∴∠C=45°,∵MN∥AC,∴∠EBD=180°﹣∠C=135°,∵∠BFD=45°,DF⊥BC,∴∠BFD=45°,BD=DF,∴∠AFD=135°,∴∠EBD=∠AFD,在△BDE和△FDA中,∵∠EBD=∠AFD,BD=DF,∠BDF=∠ADF,∴△BDE≌△FDA(ASA),∴AD=DE;
(2)DE=![]() AD,理由:
AD,理由:
如图2,过点D作DG⊥BC,交AB于点G,则∠BDE+∠GDE=90°,∵DE⊥AD,∴∠GDE+∠ADG=90°,∴∠BDE=∠ADG,∵∠BAC=90°,∠ABC=30°,∴∠C=60°,∵MN∥AC,∴∠EBD=180°﹣∠C=120°,∵∠ABC=30°,DG⊥BC,∴∠BGD=60°,∴∠AGD=120°,∴∠EBD=∠AGD,∴△BDE∽△GDA,∴![]() ,在Rt△BDG中,
,在Rt△BDG中,![]() =tan30°=
=tan30°=![]() ,∴DE=
,∴DE=![]() AD;
AD;
(3)AD=DEtanα;理由:
如图2,∠BDE+∠GDE=90°,∵DE⊥AD,∴∠GDE+∠ADG=90°,∴∠BDE=∠ADG,∵∠EBD=90°+α,∠AGD=90°+α,∴∠EBD=∠AGD,∴△EBD∽△AGD,∴![]() ,在Rt△BDG中,
,在Rt△BDG中,![]() =tanα,则
=tanα,则![]() =tanα,∴AD=DEtanα.
=tanα,∴AD=DEtanα.

 阅读快车系列答案
阅读快车系列答案