题目内容
【题目】求出符合条件的二次函数解析式:
(1)二次函数图象经过点(﹣1,0),(1,2),(0,3);
(2)二次函数图象的顶点坐标为(﹣3,6),且经过点(﹣2,10);
(3)二次函数图象与x轴的交点坐标为(﹣1,0),(3,0),与y轴交点的纵坐标为9.
【答案】(1)y=﹣2x2+x+3(2)y=4(x+3)2+6(3)y=﹣3x2+6x+9
【解析】试题分析:(1)设一般式y=ax2+bx+c,再把三个点的坐标代入得到关于a、b、c的方程组,然后解方程组求出a、b、c的值即可;
(2)由于已知顶点坐标,则可设顶点式y=a(x+3)2+6,然后把(-2,10)代入求出a即可;
(3)由于已知抛物线与x轴的两交点坐标,则可设交点式y=a(x+1)(x-3),然后把(0,9)代入求出a即可.
解:(1)设二次函数解析式为y=ax2+bx+c,
根据题意得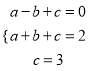 ,解得
,解得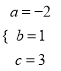 ,
,
所以二次函数解析式为y=﹣2x2+x+3;
(2)二次函数解析式为y=a(x+3)2+6,
把(﹣2,10)代入得a×(﹣2+3)2+6=10,解得a=4,
所以二次函数解析式为y=4(x+3)2+6;
(3)设二次函数解析式为y=a(x+1)(x﹣3),
把(0,9)代入得a×1×(﹣3)=9,解得a=﹣3,
所以二次函数解析式为y=﹣3(x+1)(x﹣3)=﹣3x2+6x+9.

【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.