Question

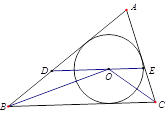
【题目】如图，⊙O是△ABC的内切圆，过点O作DE∥BC，与AB、AC分别交于点D、E.

（1）求证：BD+CE＝DE；

（2）若∠BAC=70，求∠BOC的度数

Answer 1

【答案】（1）证明见解析；（2）125°.

【解析】试题分析：（1）利用角平分线和平行线的性质易证DO=BD，EO=CE,进而得证：BD+CE=DE；

（1）由BO、CO是角平分线，可证明∠BOC=90°+∠A，即可得出结论.

试题解析：（1）∵⊙O是△ABC的内切圆

∴平分， 平分

∵DE∥BC

∴

∴

∴

（2）∵平分， 平分

∴∠OBC=∠ABC，∠OCB=∠ACB，

∴∠BOC=180°-（∠OBC+∠OCB）=180°-（∠ABC +∠ACB）=180°-（90°-∠A）=90°+∠A

∵∠BAC=70

∴∠BOC=90°+35°=125°.