题目内容
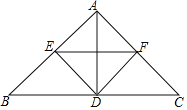
【题目】如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
(1)求证:△BDE≌△CDF;
(2)若BC=2AD,求证:四边形AEDF是正方形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)用ASA证明△BDE≌△CDF;
(2)由BC=2AD,得∠BAC=90°,从而四边形AEDF是矩形,再由AE=AF即可得证.
试题解析:
证明:(1)∵AB=AC,∴∠B=∠C,
∵EF∥BC,∴∠AEF=∠B,∠AFE=∠C,∴∠AEF=∠AFE,
∴AE=AF,∴BE=CF,
∵DE⊥AB,DF⊥AC,∴∠AED=∠AFD=90°,
在△BED和△CFD中,
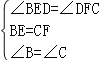 ,
,
∴△BDE≌△CDF.
(2)∵△BDE≌△CDF,∴BD=DC,DE=DF,
∵BC=2AD,∴AD=![]() BC,∴∠BAC=90°,
BC,∴∠BAC=90°,
∵DE⊥AB,DF⊥AC,∴∠EAF=∠AED=∠AFD=90°,∴四边形AEDF是矩形,
∵AE=AF,∴四边形AEDF是正方形.

【题目】2007年5月19日起,中国人民银行上调存款利率.
人民币存款利率调整表:
项 目 | 调整前年利率% | 调整后年利率% |
活期存款 | 0.72 | 0.72 |
二年期定期存款 | 2.79 | 3.06 |
储户的实得利息收益是扣除利息税后的所得利息,利息税率为20%.
(1)小明于2007年5月19日把3500元的压岁钱按一年期定期存入银行,到期时他实得利息收益是多少元?
(2)小明在这次利率调整前有一笔一年期定期存款,到期时按调整前的年利率2.79%计息,本金与实得利息收益的和为2555.8元,问他这笔存款的本金是多少元?
(3)小明爸爸有一张在2007年5月19日前存人的10000元的一年期定期存款单,为获取更大的利息收益,想把这笔存款转存为利率调整后的一年期定期存款.问他是否应该转存?请说明理由.
约定:①存款天数按整数天计算,一年按360天计算利息.
②比较利息大小是指从首次存入日开始的一年时间内.获得的利息比较.如果不转存,利息按调整前的一年期定期利率计算;如果转存,转存前已存天数的利息按活期利率计算,转存后,余下天数的利息按调整后的一年期定期利率计算(转存前后本金不变).