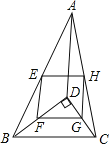Question

【题目】（概念认识）

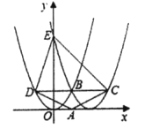
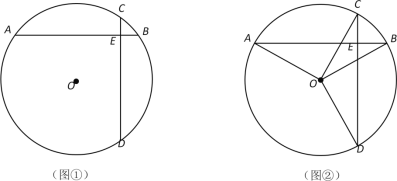
在同一个圆中两条互相垂直且相等的弦定义为“等垂弦”，两条弦所在直线的交点为等垂弦的分割点．如图①，AB、CD是⊙O的弦，AB＝CD，AB⊥CD，垂足为E，则AB、CD是等垂弦，E为等垂弦AB、CD的分割点．

（数学理解）

（1）如图②，AB是⊙O的弦，作OC⊥OA、OD⊥OB，分别交⊙O于点C、D，连接CD．求证： AB、CD是⊙O的等垂弦．

（2）在⊙O中，⊙O的半径为5，E为等垂弦AB、CD的分割点，．求AB的长度．

（问题解决）

（3）AB、CD是⊙O的两条弦，CD＝AB，且CD⊥AB，垂足为F．

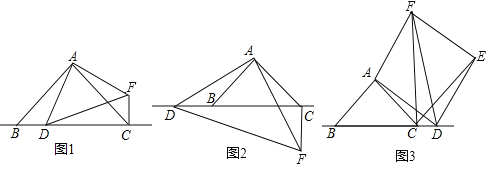
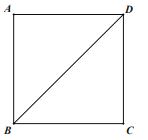
①在图③中，利用直尺和圆规作弦CD（保留作图痕迹，不写作法）．

②若⊙O的半径为r，AB＝mr（m为常数），垂足F与⊙O的位置关系随m的值变化而变化，直接写出点F与⊙O的位置关系及对应的m的取值范围．

Answer 1

【答案】（1）详见解析；（2）2；（3）①作图见解析；②当0＜m＜时，点F在⊙O外；当m＝时，点F在⊙O上；＜m≤2时，点F在⊙O内.

【解析】

（1）根据在同圆中，相等的圆心角所对的弦相等证明AB=CD，再根据同弧所对的圆周角等于它所对的圆心角的一半可证明∠ACB=∠DCB=45°，从而可得结论；

（2）分两种情况：①点E在⊙O内，作OH⊥AB，垂足为H，作OG⊥CD，垂足为G，证明△AHO≌△DGO得OH＝OG，再证明矩形OHEG为正方形结合＝证明出AH＝2OH，运用勾股定理求出OH的长即可；②点E在⊙O外，求解方法同①；

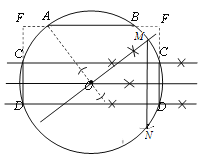
（3）①连接OA，过O作OM⊥OA交于点M，以M为圆心，以AG的长为半径画弧交于点N，连接MN，再四等分弦MN,即可作出CD=且CD ⊥AB；

②由于AB是⊙O的弦可知m≤2，再由点F在圆上时可求出m=，最后分当0＜m＜时，点F在⊙O外；当m＝时，点F在⊙O上；＜m≤2时，点F在⊙O内，三种情况进行讨论即可.

（1）如图①，连接BC，

∵OC⊥OA、OD⊥OB，

∴∠AOC＝∠BOD＝90°，

∴∠AOB＝∠COD，

∴AB＝CD，

∵＝

∴∠ABC＝∠AOC＝45°．

同理∴∠BCD＝∠BOD＝45°，

∴∠AEC＝∠ABC＋∠BCD＝90°，

即AB⊥CD，

∵AB＝CD，AB⊥CD，

∴ AB、CD是⊙O的等垂弦．

（2）如图②，若点E在⊙O内，作OH⊥AB，垂足为H，作OG⊥CD，垂足为G，

∵AB、CD是⊙O的等垂弦，

∴AB＝CD，AB⊥CD，

∴AH＝DG＝AB，OA＝OD，∠AHO＝∠DGO，

∴△AHO≌△DGO，

∴OH＝OG，

∴矩形OHEG为正方形，

∴OH＝HE ．

∵＝，

又AH＝BH，

∴AH＝2BE＝2OH，

在Rt△AOH中，AO2＝AH2＋OH2．

即(2OH)2＋OH2＝AO2＝25，

解得OH＝，则AB＝4HE＝4；

若点E在⊙O外，同理，AH＝，则AB＝2AH＝2．

（3）①如图所示，弦CD即为所求；

②∵AB是⊙O的弦，

∴AB≤2r，即m≤2，

当点F在圆上时，如图所示，

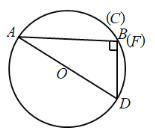
此时，AB=mr，CD=，AD=2r

由勾股定理得，

解得，

因此，当0＜m＜时，点F在⊙O外；当m＝时，点F在⊙O上；当＜m≤2时，点F在⊙O内.