Question

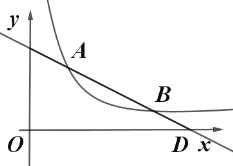
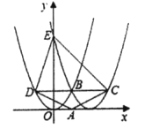
【题目】如图，在平面直角坐标系中，抛物线与的图像交于点，抛物线交轴于点，过点作轴的平行线交两抛物线于、两点．若点是轴上两抛物线顶点之间的一点，连结，，，，则四边形的面积为________（用含的代数式表示）．

Answer 1

【答案】8a

【解析】

先联立两抛物线的解析式求出点B坐标，再根据抛物线的对称性得出点D、C的坐标，进而可得CD的长，而点E坐标易求，然后利用即可求出结果．

解：解方程组，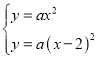

得：，

∴点B的坐标为（1，a），

∵抛物线与的对称轴分别是y轴和直线x=2，

∴D、B关于y轴对称，B、C关于直线x=2对称，

∴D点坐标为（﹣1，a），C点坐标为（3，a），

∴CD=3－（﹣1）=4，

对抛物线，当x=0时，y=4a，∴点E坐标为（0，4a），

∴．

故答案为：8a．