题目内容
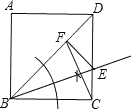
【题目】在正方形ABCD中,E是CD边上的点,过点E作EF⊥BD于F.
(1)尺规作图:在图中求作点E,使得EF=EC;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接FC,求∠BCF的度数.
【答案】(1)作图见解析;(2)∠BCF=67.5°.
【解析】
(1)作∠CBD的角平分线即可.
(2)证明BF=BC,利用等腰三角形的性质即可解决问题.
解:(1)如图,点E即为所求.
(2)∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD.
∴∠DBC=∠CDB=45°,
∵EF⊥BD,
∴∠BFE=90°.
由(1)得EF=EC,BE=BE,
∴Rt△BFE≌Rt△BCE(HL)
∴BC=BF.
∴∠BCF=∠BFC,
∴∠BCF=![]() (180°∠FBC)=67.5°.
(180°∠FBC)=67.5°.

练习册系列答案
相关题目