��Ŀ����
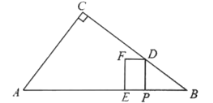
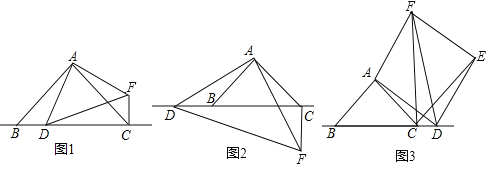
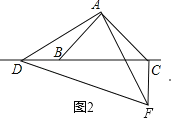
����Ŀ��ijУ���꼶��ѧ��ȤС�����о�����ֱ����������ͼ�α任ʱ�����������о����ڡ�ABC�У���BAC��90�㣬AB��AC����DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ��������ֱ��������DAF��ʹ��DAF��90�㣬����CF��
��1���۲����
��ͼ1������D���߶�BC��ʱ��
��CF��BC��λ�ù�ϵΪ�� ����
��CF��DC��BC֮���������ϵΪ�� ����ֱ��д�����ۣ���
��2����ѧ˼��
��ͼ2������D���߶�CB���ӳ�����ʱ����1���е������������Ƿ���Ȼ�������������������֤������������������д����ȷ�����ٸ���֤����
��3����չ����
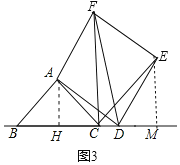
��ͼ3������D���߶�BC���ӳ�����ʱ������DAF���߶�DF���ۣ�ʹ��A���E�غϣ�����CE������֪4CD��BC��AC��2![]() ��������߶�CE�ij���
��������߶�CE�ij���
���𰸡���1���ٴ�ֱ����BC��CF+CD����2��CF��BC������BC��CD+CF�����������ۣ�CD��CF+BC�����ɼ���������3��CE��3![]() ��
��
��������
��1�����ɡ�BAC����DAF��90�㣬�Ƴ���DAB�ա�FAC������ȫ�������ε����ʼ��ɵõ����ۣ�����������ADEF�����ʿ��Ƴ���DAB�ա�FAC������ȫ�������ε����ʵõ�CF��BD����ACF����ABD��������ǵ����ʼ��ɵõ����ۣ�
��2���ɡ�BAC����DAF��90�㣬�Ƴ���DAB�ա�FAC������ȫ�������ε������Լ�����ֱ�������εĽǵ����ʿɵõ����ۣ�
��3����A��AH��BC��H����E��EM��BD��M��ͼ3��ʾ����취֤����ADH�ա�DEM��AAS�����Ƴ�EM��DH��3��DM��AH��2���Ƴ�CM��EM��3�����ɽ�����⣮
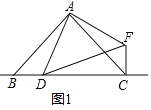
�⣺��1����
����ֱ����ADF�У�AD��AF��
�ߡ�BAC����DAF��90����
���BAD����CAF��
����DAB����FAC��
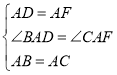 ��
��
���DAB�ա�FAC��SAS����
���B����ACF��
���ACB+��ACF��90������BC��CF��
�ڡ�DAB�ա�FAC��
��CF��BD��
��BC��BD+CD��
��BC��CF+CD��
�ʴ�Ϊ����ֱ��BC��CF+CD��
��2��CF��BC������BC��CD+CF�����������ۣ�CD��CF+BC���������£�
������ֱ����ADF�У�AD��AF��
�ߡ�BAC����DAF��90����
���BAD����CAF��
����DAB����FAC��
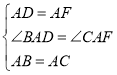 ��
��
���DAB�ա�FAC��SAS����
���ABD����ACF��
�ߡ�BAC��90����AB��AC��
���ACB����ABC��45����
���ABD��180����45����135����
���BCF����ACF����ACB��135����45����90����
��CF��BC��
��CD��DB+BC��DB��CF��
��CD��CF+BC��
��3����A��AH��BC��H����E��EM��BD��M��ͼ3��ʾ��
�ߡ�BAC��90����AB��AC��2![]() ��
��
��BC��![]() AB��4��AH��BH��CH��
AB��4��AH��BH��CH��![]() BC��2��
BC��2��
��CD��![]() BC��1��
BC��1��
��DH��CH+CD��3��
���ı���ADEF�������Σ�
��AD��DE����ADE��90����
��BC��CF��EM��BD��EN��CF��
���ı���CMEN�Ǿ��Σ�
��NE��CM��EM��CN��
�ߡ�AHD����ADC����EMD��90����
���ADH+��EDM����EDM+��DEM��90����
���ADH����DEM��
����ADH����DEM��
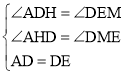 ��
��
���ADH�ա�DEM��AAS����
��EM��DH��3��DM��AH��2��
��CM��EM��3��
��CE��![]() ��3
��3![]() ��
��

����Ŀ���л�������ԴԶ�������л����֣�Ԣ�����.Ϊ�����л����㴫ͳ�Ļ���ij��ѧ��������֯��һ��ȫУ2000��ѧ���μӵ���������д������.Ϊ�˽Ȿ�δ����ijɼ���ѧУ�����������ȡ������200��ѧ���ijɼ���Ϊ��������ͳ�ƣ��Ƴ����²�������ͳ��ͼ����
�ɼ�x���֣������� | Ƶ�����ˣ� | Ƶ�� |
50��x<60 | 10 | 0.05 |
60��x<70 | 30 | 0.15 |
70��x<80 | 40 | 0.2 |
80��x<90 | m | 0.35 |
90��x<100 | 50 | n |
Ƶ���ֲ�ֱ��ͼ
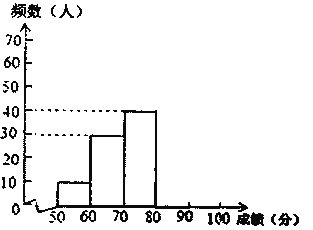
������������Ϣ���ش��������⣺
��1��m=________��n=________��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����200��ѧ���ɼ�����λ��������________�����Σ�
��4�����ɼ���90�����ϣ�����90�֣�Ϊ�������ȣ�������Ƹ�У�μӱ��α�����2000��ѧ���гɼ����������ȵ�Լ�ж����ˣ�