题目内容
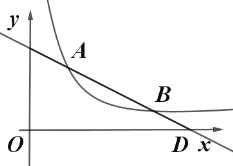
【题目】一辆货车从A地出发以每小时80km的速度匀速驶往B地，一段时间后，一辆轿车从B地出发沿同一条路匀速驶往A地．货车行驶3小时后，在距B地160km处与轿车相遇．图中线段表示货车离B地的距离y1与货车行驶的时间x的关系．
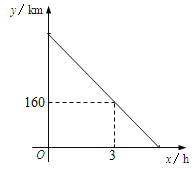
（1）AB两地之间的距离为 km；
（2）求y1与x之间的函数关系式；
（3）若两车同时到达各自目的地，在同一坐标系中画出轿车离B地的距离y2与货车行驶时间x的函数图像，用文字说明该图像与x轴交点所表示的实际意义．
【答案】（1）400；（2）y1＝－80x＋400；（3）详见解析，货车从A地出发
小时后，轿车从B地出发．
【解析】
（1）根据货车行驶的路程+货车离B地的路程即可得出A、B两地之间的距离；
（2）根据函数图象经过的点设出一次函数的解析式用待定系数法求一次函数的解析式即可；
（3）作出一次函数的图象并根据图象得到交点坐标所表示的意义是货车从A地出发小时后轿车从B地出发．
（1）AB两地之间的距离为：80×3+160=400km，
故答案为：400；
（2）因为货车从A地出发以每小时80km的速度匀速驶往B地，
所以y1+80x=b，代入点（3，160），得b=400．
∴y1=-80x+400；
（3）如图，线段y2即为所求的图像；
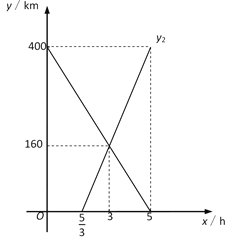
货车行驶的时间为400÷80＝5h，则可求设y2的函数表达式为y2=mx+n
把（5，400），（3，160）分别代入y2=mx+n得，
解得，
∴y2＝120x－200，
当y=0时，x=，
故该图像与x轴交点坐标为（，0）．
它表示的实际意义：货车从A地出发小时后，轿车从B地出发．
【题目】工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，请将下列过程补充完整：
收集数据：
从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如下：
整理、描述数据：
按如下分数段整理、描述这两组样本数据：
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
（说明：成绩80分及以上为生产技能优秀，70—79分为生产技能良好，60—69分为生产技能合格，60分以下为生产技能不合格）
分析数据：
两组样本数据的平均数、中位数、众数如下表所示：
部门 | 平均数 | 中位数 | 众数 |
甲 | 78．3 | 77．5 | |
乙 | 78 | 81 |
得出结论：
．估计乙部门生产技能优秀的员工人数约为 ．
．可以推断出 部门员工的生产技能水平高．理由为 ．
（至少从两个不同的角度说明推断的合理性）
