题目内容
【题目】在平面直角坐标系中,已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,求函数图像的顶点坐标(用含
时,求函数图像的顶点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)当y最大值为1时,且![]() ,求整数
,求整数![]() 的值;
的值;
(3)当直线![]() 与函数
与函数![]() 的图像只有一个公共点时,求
的图像只有一个公共点时,求![]() 的取值范围;
的取值范围;
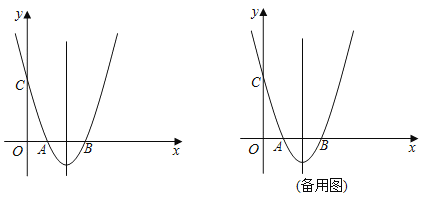
(4)设点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上的正半轴上,已知点
轴上的正半轴上,已知点![]() ,以
,以![]() 为边做正方形
为边做正方形![]() ,当函数
,当函数![]() 的图像与正方形
的图像与正方形![]() 的边有两个公共点时,直接写出
的边有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() ;(4)
;(4)![]() 或
或![]() 或
或![]()
【解析】
(1)把函数![]() 配方成顶点式即可求得;
配方成顶点式即可求得;
(2)分两类情况:当![]() 时,
时, ![]() ,当
,当![]() 时,
时,![]() ,结合
,结合![]() ,即可算出n的值;
,即可算出n的值;
(3)分两类情况:当![]() 时,交点即是抛物线的顶点,当
时,交点即是抛物线的顶点,当![]() 时,满足
时,满足![]() 即可;
即可;
(4)数形结合的方法,看两个交点在哪些边上,分类讨论,结合点的坐标即可算出n的取值范围.
(1)![]()
所以当![]() 时,顶点坐标为
时,顶点坐标为![]()
(2) 当![]() 时,
时, ![]() ;
;
当![]() 时,
时,![]()
![]() 且是整数
且是整数
所以![]() 或
或![]() 或
或![]()
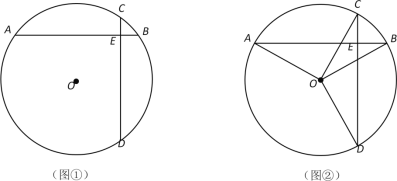
(3)当![]() 时, 交点即是抛物线的顶点,
时, 交点即是抛物线的顶点,![]() ,如图①
,如图①
解得:![]() (舍去),
(舍去),![]()
当![]() 时,满足
时,满足![]() 即可,解得
即可,解得![]() 如图②
如图②
综上得,n的取值范围是![]() 或
或![]()
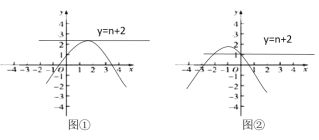
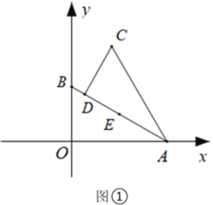
(4)
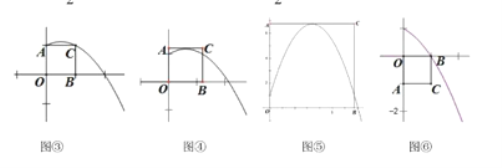
当两个交点都在AC上时,如图③,则经过C点(2n,2n),得:![]() ;
;
当一个交点在OA上,一个交点在BC上时,如图④,则顶点在AC之下,即:![]() ;
;
当交点在OB和BC上时,则![]() ,且抛物线在B点下方,如图⑥即:
,且抛物线在B点下方,如图⑥即:![]() 或
或![]() (舍去),
(舍去),
综上可得,n的取值范围是:![]() 或
或![]() 或
或![]() .
.

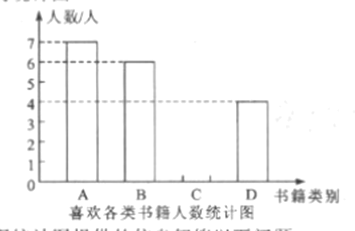
【题目】工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,请将下列过程补充完整:
收集数据:
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:

整理、描述数据:
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70—79分为生产技能良好,60—69分为生产技能合格,60分以下为生产技能不合格)
分析数据:
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | |
乙 | 78 | 81 |
得出结论:
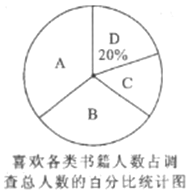
![]() .估计乙部门生产技能优秀的员工人数约为 .
.估计乙部门生产技能优秀的员工人数约为 .
![]() .可以推断出 部门员工的生产技能水平高.理由为 .
.可以推断出 部门员工的生产技能水平高.理由为 .
(至少从两个不同的角度说明推断的合理性)
【题目】某种水果按照果径大小可分为4个等级:标准果、优质果、精品果、礼品果,某采购商从采购的一批该种水果中随机抽取100个,利用它的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
用样本估计总体,果园老板提出两种购销方案给采购商参考,
方案1:不分类卖出,售价为20元/个;
方案2:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/个) | 16 | 18 | 22 | 24 |
(1)从采购商的角度考虑,应该采用哪种购销方案?
(2)若采购商采购的该种水果的进价不超过20元/个,则采购商可以获利,现从这种水果的4个等级中任选2种,按方案2进行购买,求这2种等级的水果至少有一种能使采购商获利的概率.