题目内容
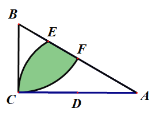
【题目】如图，在平面直角坐标系中，点P（2，5）、Q（a，b）（a＞2）在“函数y＝
（x＞0）的图象上，过点P分别作x轴、y轴的垂线，垂足为A、B；过点Q分别作x轴、y轴的垂线，垂足为C、D．QD交PA于点E，随着a的增大，四边形ACQE的面积（ ）
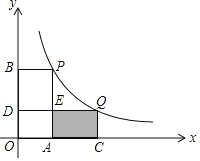
A.增大B.减小C.先减小后增大D.先增大后减小
【答案】A
【解析】
根据题意先用含a，b的式子表示四边形ACQE的面积得S四边形ACQE＝ACCQ＝ab﹣2b，根据P，Q都在函数y＝
的图象上得ab＝k＝10，且b随a的增大而减小，进而可得答案.
解：∵点P（2，5）、Q（a，b）（a＞2），
∴AC＝a﹣2，CQ＝b，
则S四边形ACQE＝ACCQ＝（a﹣2）b＝ab﹣2b，
∵点P（2，5）、Q（a，b）（a＞2）在“函数y＝
（x＞0）的图象上，
∴ab＝k＝10（常数），
∴S四边形ACQE＝10﹣2b，
∴当a＞2时，b随a的增大而减小，
∴S四边形ACQE＝10﹣2b随a的增大而增大.
故选：A．
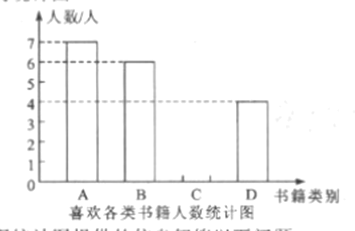
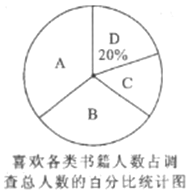
名校课堂系列答案
【题目】中华文明，源远流长，中华汉字，寓意深广.为传承中华优秀传统文化，某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩，学校德育处随机抽取了其中200名学生的成绩作为样本进行统计，制成如下不完整的统计图表：
成绩x（分）分数段 | 频数（人） | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图
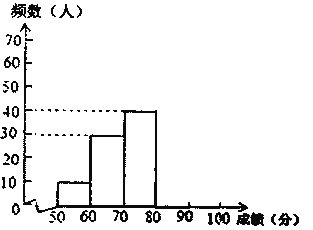
根据所给的信息，回答下列问题：
（1）m=________；n=________；
（2）补全频数分布直方图；
（3）这200名学生成绩的中位数会落在________分数段；
（4）若成绩在90分以上（包括90分）为“优”等，请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人？
