题目内容
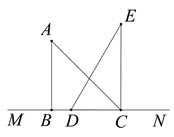
【题目】如图，已知△ABC和△BDE都是等边三角形，且A，E，D三点在一直线上．请你说明DA﹣DB=DC．
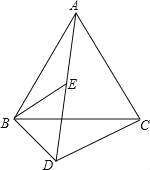
【答案】证明见解析．
【解析】试题分析：根据等边三角形的性质，可得AB与BC的关系，BD、BE、DE的关系，根据三角形全等的判定，可得△ABE与△CBD的关系，根据全等三角形的性质，可得对应边相等，根据线段的和差，等量代换，可得证明结果．
试题解析：
△ABC和△BDE都是等边三角形
∴AB=BC，BE=BD=DE（等边三角形的边相等），
∠ABC=∠EBD=60°（等边三角形的角是60°）．
∴∠ABC﹣∠EBC=∠EBD﹣∠EBC
∠ABE=CBD （等式的性质），
在△ABE和△CBD中，
，
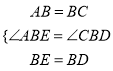∴△ABE≌△CBD（SAS）
∴AE=DC（全等三角形的对应边相等）．
∵AD﹣DE=AE（线段的和差）
∴AD﹣BD=DC（等量代换）．
练习册系列答案
全能测控期末小状元系列答案
相关题目
