题目内容
【题目】如图,将一幅三角板按照如图所示的位置放置在直线![]() 上,
上, ![]() =
=![]() =45°,
=45°,![]() =
=![]() =90°,
=90°,![]() =30°,
=30°,![]() =60°.将含45°锐角的三角板
=60°.将含45°锐角的三角板![]() 固定不动,含30°锐角的三角板
固定不动,含30°锐角的三角板![]() 绕点
绕点![]() 顺时针旋转1周,在此过程中:
顺时针旋转1周,在此过程中:
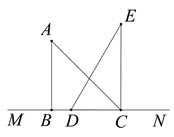
(1)如图,当点![]() 在
在![]() 内部时,连接
内部时,连接![]() .
.
①若![]() 平分
平分![]() ,试问
,试问![]() 是否也平分
是否也平分![]() ?请说明理由.
?请说明理由.
②若![]() ,
, ![]() ,
, ![]() ,试探究
,试探究![]() 、
、![]() 、
、![]() 这三者之间有什么数量关系?请用一个含
这三者之间有什么数量关系?请用一个含![]() 、
、![]() 、
、![]() 的等式来表达,并说明理由.
的等式来表达,并说明理由.
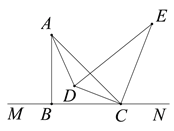
(2)如图, ![]() 是
是![]() 的角平分线,当
的角平分线,当![]() 所在直线与
所在直线与![]() 所在直线互相垂直时,请直接写出
所在直线互相垂直时,请直接写出![]() 的度数.
的度数.

【答案】(1)①当CD平分∠ACB时,CE也平分∠ACN;②![]()
![]()
![]() =30°;(2)
=30°;(2)![]() =52.5°或127.5°
=52.5°或127.5°
【解析】试题分析:(1)①根据角平分线的定义,即可求解;
②根据角的和差关系即可求解;
(2)利用四边形的内角和等于360°即可求解.
试题解析:(1)当CD平分∠ACB时,CE也平分∠ACN,
理由如下:
∵CD平分∠ACB,
∴∠ACD=![]() ∠ACB,
∠ACB,
∵∠ACD+∠ACE=90°,
∴∠ACE=90°-∠ACD=90°-![]() ∠ACB=
∠ACB=![]() (180°-∠ACB)=
(180°-∠ACB)= ![]() ∠ACN,
∠ACN,
∴CE平分∠ACN.
(2)![]()
![]()
![]() =30°,
=30°,
理由:由题知![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() +60°,
+60°,![]() ,
, ![]() ,∵∠ADC+∠CAD+∠ACD=180°,∴
,∵∠ADC+∠CAD+∠ACD=180°,∴![]() +60°+
+60°+![]() +
+![]() =180°,∴
=180°,∴![]()
![]()
![]() =30°
=30°
(3)![]() =52.5°或127.5°
=52.5°或127.5°

练习册系列答案
相关题目