题目内容
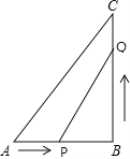
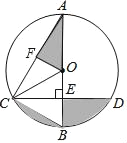
【题目】如图,AB为⊙O的直径,CD是弦,AB⊥CD于点E,OF⊥AC于点F,BE=OF.
(1)求证:△AFO≌△CEB;
(2)若BE=4,CD=8![]() ,求:
,求:
①⊙O的半径;
②求图中阴影部分的面积.
【答案】(1)见解析;(2)①8;②![]()
【解析】
(1)根据垂径定理知BC=BD,再利用圆周角定理知∠A=∠DCB,而∠AFO=∠CEB,故可证明△AFO≌△CEB;(2)①利用垂径定理得出CE=4![]() ,设 OC=r,则 OE=r﹣4,根据勾股定理可得r2=(r﹣4)2+(4
,设 OC=r,则 OE=r﹣4,根据勾股定理可得r2=(r﹣4)2+(4![]() )2,即可求出r;②根据阴影部分等于扇形OABD的面积减去△CDO的面积即可求出.
)2,即可求出r;②根据阴影部分等于扇形OABD的面积减去△CDO的面积即可求出.
(1)证明:∵AB 为⊙O 的直径,AB⊥CD,
∴BC=BD,
∴∠A=∠DCB,
∴OF⊥AC,
∴∠AFO=∠CEB,
∵BE=OF,
∴△AFO≌△CEB(AAS).
(2)①∵AB 为⊙O 的直径,AB⊥CD,
∴CE=![]() CD=4
CD=4![]()
设 OC=r,则 OE=r﹣4,
∴r2=(r﹣4)2+(4![]() )2
)2
∴r=8.
②连结 OD.
∵OE=4=![]() OC,
OC,
∴∠OCE=30°,∠COB=60°,
∴∠COD=120°,
∵△AFO≌△CEB,
∴S△AFO=S△BCE,
∴S阴=S扇形OCD﹣S△OCD
=![]() ﹣
﹣![]()
=![]() ﹣16
﹣16![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目