题目内容
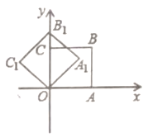
【题目】如图，在平面直角坐标系中，将正方形
绕点
逆时针旋转
后得到正方形
，依此方式，绕点连续旋转2019次得到正方形
，如果点
的坐标为（1，0），那么点
的坐标为________．
【答案】
【解析】
根据图形可知：点B在以O为圆心,以OB为半径的圆上运动,由旋转可知：将正方形OABC绕点O逆时针旋转45后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45，可得对应点B的坐标，根据规律发现是8次一循环，可得结论.
∵四边形OABC是正方形，且OA=1，∴B(1,1),连接OB，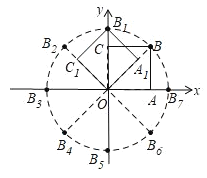
由勾股定理得：OB=
，
由旋转得：OB=OB1=OB2=OB3=…=，
∵将正方形OABC绕点O逆时针旋转45后得到正方形OA1B1C1，
相当于将线段OB绕点O逆时针旋转45,依次得到∠AOB=∠BOB1=∠B1OB2=…=45，
∴B1(0,
),B2(1,1),B3(,0)，…，
发现是8次一循环，所以2019÷8=252…3，
∴点B2019的坐标为(,0)
练习册系列答案
相关题目
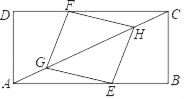
【题目】如图，矩形ABCD中，点E，F分别在边AB与CD上，点G、H在对角线AC上，AG＝CH，BE＝DF．
（1）求证：四边形EGFH是平行四边形；
（2）若EG＝EH，AB＝8，BC＝4．求AE的长．
【题目】有20筐白菜，以每筐30千克为标准，超过千克数记作正数，不足的千克数记作负数，称后的记录如下表：
与标准质量的差值（单位：千克） |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 4 | 2 | 3 | 6 |
（1）20筐白菜中，最重的一筐比最轻的一筐重 千克；
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价3.5元，则出售这20筐白菜可卖多少元？