题目内容
【题目】如图,AC是□ ABCD的对角线,延长BA至点E,使AE=AB,连接DE.
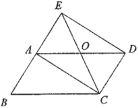
(1)求证:四边形ACDE是平行四边形;
(2)连接EC交AD于点O,若∠EOD=2∠B,求证:四边形ACDE是矩形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由平行四边形的性质可得AB=CD,AB∥CD,结合AE=AB由一组对边平行且相等的四边形是平行四边形可证四边形ACDE是平行四边形;
(2)由三角形的外角可证∠ADC=∠OCD,可得OC=OD,即可得AD=EC,可证四边形ACDE是矩形.
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AE=AB,
∴AE=CD,且AB∥CD,
∴四边形ACDE是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴∠B=∠ADC,
∵∠EOD=2∠B
∴∠EOD=2∠ADC,且∠EOD=∠ADC+∠OCD,
∴∠ADC=∠OCD,
∴OC=OD,
∵四边形ACDE是平行四边形,
∴AO=DO,EO=CO,
∴AD=CE,
∴四边形ACDE是矩形.

练习册系列答案
相关题目
【题目】用一样长的小木棒按下图中的方式搭图形.
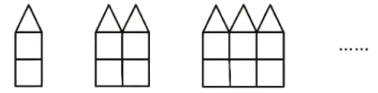
(1)按图示规律填空:
图形标号 | ① | ② | ③ | … |
小木棒的根数 | 9 | … |
(2)按照这种规律搭下去,搭第![]() 个图形需要________根小木棒;
个图形需要________根小木棒;
(3)请求出搭第100个图形需要的小木棒的根数.