题目内容
【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点达到终点后,另外一点也随之停止运动.
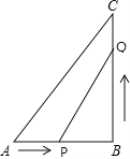
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,当P、Q出发几秒时,△PBQ的面积最大,最大面积是多少?
【答案】(1)1秒;(2)2秒;(3)![]() 秒后,△PBQ的面积最大,最大面积是
秒后,△PBQ的面积最大,最大面积是![]() cm2.
cm2.
【解析】
(1)设t秒后,△PBQ的面积等于4cm2,根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长可列方程求解;
(2)利用勾股定理列出方程求解即可;
(3)结合(1)列出函数关系式,化成顶点是即可.
解:(1)设t秒后,△PBQ的面积等于4cm2,
则:AP=tcm,BP=(5-t)cm; BQ=2tcm.
S△PBQ=![]() BP×BQ,即4=
BP×BQ,即4=![]() ×(5-t)×2t,
×(5-t)×2t,
解得:t=1或4.(t=4秒不合题意,舍去)
答:1秒后,△PBQ的面积等于4cm2;
(2)设t秒后,△PBQ中PQ的长度等于5cm,即PQ=5,
则PQ2=25=BP2+BQ2,即25=(5-t)2+(2t)2,
解得:t=0(舍)或2.
答:2秒后,PQ的长度为5cm;
(3)设面积为Scm2,时间为t,
则S =![]() BP×BQ=
BP×BQ=![]() ×(5-t)×2t =-t2+5t= -(t-
×(5-t)×2t =-t2+5t= -(t-![]() )2+
)2+![]() ,
,
答:![]() 秒后,△PBQ的面积最大,最大面积是
秒后,△PBQ的面积最大,最大面积是![]() cm2.
cm2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目