题目内容
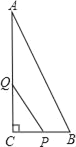
【题目】如图,△ABC中,∠C=90°,AC=16cm,BC=8cm,一动点P从点C出发沿着CB方向以2cm/s的速度运动,另一动点Q从A出发沿着AC边以4cm/s的速度运动,P、Q两点同时出发,运动时间为t(s).
(1)若△PCQ的面积是△ABC面积的![]() ,求t的值?
,求t的值?
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
【答案】(1) 2s;(2)不能.
【解析】
(1)根据三角形的面积公式可以得出△ABC面积为:![]() 8×16=64,△PCQ的面积为
8×16=64,△PCQ的面积为![]() 2t(16﹣4t),由题意列出方程解答即可;
2t(16﹣4t),由题意列出方程解答即可;
(2)由等量关系S△PCQ![]() S△ABC列方程求出t的值,但方程无解.
S△ABC列方程求出t的值,但方程无解.
(1)∵S△PCQ![]() 2t(16﹣4t),S△ABC
2t(16﹣4t),S△ABC![]() 8×16=64,∴
8×16=64,∴![]() 2t(16﹣4t)=64
2t(16﹣4t)=64![]() ,整理得:t2﹣4t+4=0,解得:t=2.
,整理得:t2﹣4t+4=0,解得:t=2.
答:当t=2s时△PCQ的面积为△ABC面积的![]() ;
;
(2)当△PCQ的面积与四边形ABPQ面积相等,即:当S△PCQ![]() S△ABC时,
S△ABC时,![]() 2t(16﹣4t)=64
2t(16﹣4t)=64![]() ,整理得:t2﹣4t+8=0,△=(﹣4)2﹣4×1×8=﹣16<0,∴此方程没有实数根,∴△PCQ的面积不能与四边形ABPQ面积相等.
,整理得:t2﹣4t+8=0,△=(﹣4)2﹣4×1×8=﹣16<0,∴此方程没有实数根,∴△PCQ的面积不能与四边形ABPQ面积相等.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目