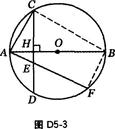
题目内容
(满分l4分)如图,已知AB为⊙O的直径,弦CD⊥AB,垂足为点H.
(1)求证:AH·AB=AC2;
(2)若过点A的直线与弦CD(不含端点)相交于点E,与⊙O相交于点F,求证:AE·AF=AC2;
(3)若过点A的直线与直线CD相交于点P,与⊙O相交于点Q,判断AP·AQ=AC2是否成立(不必证明).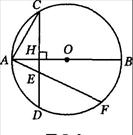
(1)求证:AH·AB=AC2;
(2)若过点A的直线与弦CD(不含端点)相交于点E,与⊙O相交于点F,求证:AE·AF=AC2;
(3)若过点A的直线与直线CD相交于点P,与⊙O相交于点Q,判断AP·AQ=AC2是否成立(不必证明).

(1)证明:连结CB,∵AB是⊙O的直径,∴∠ACB=90°. ……2分
而∠CAH=∠BAC,∴△CAH∽△BAC. ……4分
∴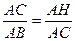 ,即AH·AB=AC2. ……5分
,即AH·AB=AC2. ……5分
(2)证明:连结FB,易证△AHE∽△AFB, ……8分
∴AE·AF=AH·AB, ……10分
∴AE·AF=AC2. ……12分
(也可连结CF,证△AEC∽△ACF)
(3)结论AP·AQ=AC2成立.

而∠CAH=∠BAC,∴△CAH∽△BAC. ……4分
∴
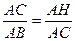 ,即AH·AB=AC2. ……5分
,即AH·AB=AC2. ……5分(2)证明:连结FB,易证△AHE∽△AFB, ……8分
∴AE·AF=AH·AB, ……10分
∴AE·AF=AC2. ……12分
(也可连结CF,证△AEC∽△ACF)
(3)结论AP·AQ=AC2成立.
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的半径分别为
的半径分别为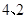 ,且
,且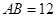 ,若做一
,若做一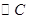 使得三圆的圆心在同一直线上,且
使得三圆的圆心在同一直线上,且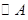 外切,
外切, 相交于两点,则
相交于两点,则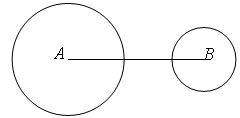
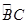 上一点,若∠CEA=28°,则
上一点,若∠CEA=28°,则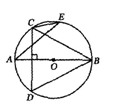
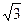 ,BC=1,求⊙O的半径.
,BC=1,求⊙O的半径.